SERIE 3
LEY DE GAUSS
Física III
Bajar
la serie en Word
 Bajar Acrobat Reader |
Lector del
formato de archivos portátiles PDF. Este formato hace posible leer documentos íntegros con textos, imágenes, fuentes y multimedia. |
M.C. Luis Alfonso Domínguez Carballo
SERIE 3 LEY DE
GAUSS Física III
M.C. Luis Alfonso Domínguez
Carballo
| Preguntas: |
|
| 1.- | Considere
la superficie gaussiana que rodea parte de la
distribución de carga mostrada en la figura (a) ¿Cuál de las cargas contribuye
al campo eléctrico en el punto P? (b) El valor obtenido para el flujo a través
de la superficie, calculado usando únicamente el campo debido a q1 y
a q2, ¿sería mas grande que, igual a, o menor que el obtenido usando
el campo total?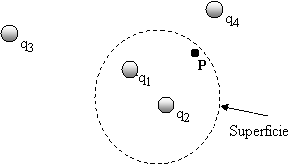
|
|
2. -
|
Una
carga puntual está situada en el centro de una superficie gaussiana
esférica. ¿Cambia Фt (a) si la superficie se sustituye por un
cubo del mismo volumen, (b) si la esfera se sustituye por un cubo de la décima
parte del volumen, (C) si la carga se mueve fuera del centro en la esfera
original y permanece adentro, (d) si la carga se mueve justo afuera de la
esfera original, (e) si se sitúa una segunda carga cerca y afuera de la esfera
original, y (f) si se sitúa una segunda carga adentro de la superficie gaussiana?
|
| 3.- | Una
superficie encierra a un dipolo eléctrico ¿Qué puede usted decir acerca de ФE
para esta superficie?
|
| 4.- | ¿Es
E necesariamente cero dentro de un globo de hule cargado, si su forma es (a)
esférica o (b) alargada? Para cada forma suponga que la carga está distribuida
uniformemente sobre la superficie. ¿Cómo cambiaría la situación, de ser así, si
el globo tuviese una capa delgada de pintura conductora en su superficie
externa?
|
| 5.- | Un
conductor hueco, aislado y grande contiene una carga positiva. A través de una
pequeña abertura en la parte superior del conductor se hace descender una
pequeña bola de metal que tiene una carga negativa de la misma magnitud, de
manera que toque la superficie interior, y luego se retira. ¿Cuál es, entonces,
la carga en (a) el conductor y (b) la bola?
|
| 6.- | Una
carga puntual positiva q está situada en el centro de una esfera de metal
hueca. ¿Qué cargas aparecen en (a) la superficie interna y en (b) la superficie
externa de la esfera? (c) si acercamos un objeto metálico (descargado) a la
esfera, ¿cambiarán sus respuestas de (a) y (b) anteriores? ¿Cambiará el modo en
que está distribuida la carga sobre la esfera?
|
| 7.- | ¿Cómo
puede ser retirada completamente la carga en exceso de un cuerpo conductor
pequeño?
|
| 8.- | Conforme
usted penetra en una esfera de carga uniforme, E debe disminuir puesto que hay
menos carga dentro de una esfera dibujada a lo largo del punto de observación.
Por otra parte, E debe aumentar porque usted está mas cerca del centro de esta
carga. ¿Cuál efecto es dominante, y por que? |
| Problemas | |
| 1.- | Un cubo con
aristas de 1.4 m, está orientado como se muestra en la figura en una región de campo eléctrico uniforme.
Encuentre el flujo eléctrico, expresado en N7C, está dado por (a) 6i, (b)
–2j y (c) –3i + 4k. (d) Calcule el flujo total a través del cubo
para cada uno de estos campos.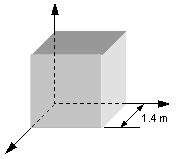
|
| 2.- | La carga en un
conductor aislado originalmente descargado se separan al sostener una barra
cargada positivamente muy cerca de él, como se muestra en la figura. Calcule el
flujo para las cinco superficies gaussianas
mostradas. Suponga que la carga negativa inducida sobre el conductor es igual a
la carga positiva q sobre la barra.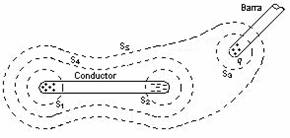
|
| 3.- | Una carga
puntual de 1.84 μC está en el centro de una superficie gaussiana
cúbica de 55 cm de arista. Halle Ф a través de la superficie.
|
| 4.- |
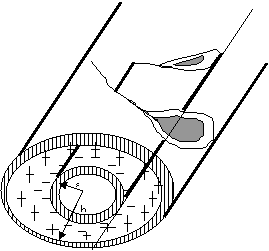
Una red para
cazar mariposas está en un campo eléctrico E uniforme como se muestra en
la figura . El aro, un círculo de radio a, está alineado perpendicularmente al campo. Halle
el flujo eléctrico de la red, respecto a la normal hacia fuera.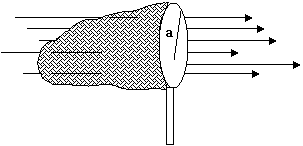
|
| 5.- | Experimentalmente
se determina que el campo eléctrico en cierta región de la atmósfera de la
Tierra está dirigido verticalmente hacia abajo. A una altitud de 300 m el campo
es de 58 N/C y a una altitud de 200 m es de 110 N/C. Calcule la cantidad neta
de carga contenida en un cubo de 100 m de arista ubicado a una altitud entre
200 y 300 m. Desprecie la curvatura de la Tierra.
|
| 6.- | Una carga
puntual q está situada en una esquina de un cubo de arista a.
¿Cuál es el flujo Ф a través de cada una de las caras del cubo? (Sugerencia:
Utilice la ley de Gauss y los argumentos de simetría).
|
| 7.- | Las componentes
del campo eléctrico en la figura son Ex = bx½, Ey = Ez
= 0, donde b = 8830 N/C m½. Calcule (a) el flujo Ф, a través del cubo y (b)
la carga dentro del cubo. Suponga que a = 13.0 cm.
|
| 8.- | Una esfera
conductora uniformemente cargada de 1.22 m de radio tiene una densidad de carga
superficial de 8.13 uC/m2. (a)
Halle la carga en la esfera. (b) ¿Cuál es el flujo eléctrico total que
sale de la superficie de la esfera? (c) Calcule el campo eléctrico en la
superficie de la esfera.
|
| 9.- | Una esfera
conductora que contiene una carga Q está rodeada por un cascarón
conductor. (a) ¿Cuál es la carga neta en la superficie interna del
cascarón?. (b) Se coloca otra carga q
tiene afuera del cascarón?. (c) Si q se
mueve a una posición entre el cascarón y la esfera, ¿cuál es la carga neta en
la superficie interna del cascarón?. (d) ¿Son
sus respuestas válidas si la esfera y el cascarón no son concéntricos?
|
| 10.- | Dos láminas no
conductoras largas y delgadas de carga positiva están una frente a la otra como
en la figura. ¿Cuál es E en los puntos (a) a la izquierda de las
láminas, (b) entre ellas y (c) a la derecha de las láminas?
Suponga la misma densidad superficial de carga σ para cada lámina.
Considere únicamente los puntos que no estén cerca de los extremos cuya
distancia a partir de las láminas es pequeña comparada con las dimensiones de
la lámina.
|
| 11.- | Dos placas
metálicas grandes están una frente a la otra como en la figura y contienen
cargas con densidad superficial de carga +σ y -σ, respectivamente, sobre sus
superficies internas. Determine E en los puntos (a) a la izquierda de
las láminas, (b) entre ellas, y (c) a la derecha de las láminas. Considere sólo
los puntos no cercanos a los extremos cuyas distancias a partir de las láminas
son pequeñas comparadas con las dimensiones de la lámina.
|
| 12.- | Un electrón
permanece estacionario en un campo eléctrico dirigido hacia abajo en el campo
gravitatorio de la Tierra. Si el campo eléctrico se debe a la carga sobre dos
placas conductoras paralelas y grandes, cargadas opuestamente y separadas por
2.3 cm, ¿cuál es la densidad superficial de carga, supuesta como uniforme,
sobre las placas? |
| 13.- | Una esfera
pequeña cuya masa m es de 1.12 mg contiene una
carga q = 19.7 nC. Cuelga en el campo
gravitatorio de la Tierra de un hilo de seda que forma un ángulo θ = 27.4°
con una lámina grande no conductora y uniformemente cargada como en la figura.
Calcule la densidad de carga uniforme σ para la lámina.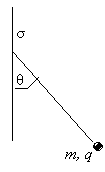
|
| 14.- | Dos esferas huecas
cargadas, delgadas y concéntricas, tienen radios de 10.0 cm y 15.0 cm. La
carga en la esfera interna es de 40.6 nC y la de
la esfera externa de 19.3 nC. Halle el campo
eléctrico (a) en r = 12.0
cm, (b) en r = 22.0cm
y (c) en r = 8.18 cm del
centro de las esferas.
|
| 15.- | Un alambre delgado,
recto y muy largo, tiene –3.60 nC/m de carga
negativa fija. El alambre se rodeará de un cilindro uniforme de carga
positiva, de 1.50 cm de radio, coaxial con el alambre. La densidad
volumétrica de carga ρ del cilindro se escoge de modo que el campo
eléctrico neto afuera del cilindro sea cero. Calcule la densidad de carga
σ positiva requerida.
|
| 16.- | La figura muestra una carga +q dispuesta
como una esfera conductora uniforme de radio a y situada en el
centro de una esfera hueca conductora de radio interior b y radio
exterior c. La esfera hueca exterior contiene una carga de – q.
Halle E(r) en las ubicaciones (a) dentro de la esfera (r
< a), (b) entre la esfera sólida y la hueca (a < r < b),
(c) dentro de la esfera hueca (b < r < c), y (d)
afuera de la esfera hueca (r < c), (e) ¿Cuáles cargas
aparecen en las superficies interna y externa de la esfera hueca?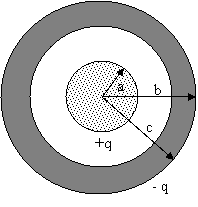
|
| 17.- | La figura muestra una carga puntual q = 126
nC en el centro de una cavidad esférica de 3.66
cm de radio en un trozo de metal. Use la ley de Gauss para hallar el campo
eléctrico (a) en el punto P1, en un punto medio entre el
centro y la superficie, y (b) en el punto P2.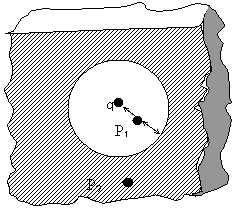
|
| 18.- | La figura 10
muestra la sección a través de un tubo metálico de pared delgada de radio R,
que contiene una carga λ por unidad de longitud en su superficie.
Deduzca expresiones de E para varias distancias r del eje
del tubo, considerando tanto (a) r > R como (b) r
< R. (c) Dibuje los resultados para la zona entre r =
0 y
r = 5.0 cm, suponiendo que λ = 2.0x19-8 C/m
y R = 3.0cm. (Sugerencia: Utilice las superficies gaussianas cilíndricas, coaxiales con el tubo de
metal.)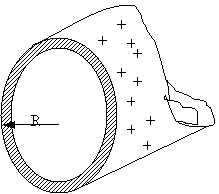
|
| 19.- | La figura muestra una
sección a través de dos cilindros concéntricos largos y delgado
de radios a y b. Los cilindros contienen cargas λ por unidad de longitud iguales y opuestas.
Use la ley de Gauss y demuestre (a) que E = 0 para r < a, y (b) que entre los cilindros E
está dada por: E
= 1 . l 2pe0 r
|
