UN PROBLEMA QUE PARECE FÁCIL

 

Un recipiente de treinta vasos de capacidad está lleno de agua. Ponemos un vaso debajo del grifo que tiene el recipiente, abrimos y, reloj en mano, observamos cuánto tiempo tarda el vaso en llenarse hasta los bordes. Supongamos que tar­da medio minuto. Nos planteamos la pregunta: ¿cuánto tiempo tardará el recipiente en vaciarse por completo, si dejamos el gri­fo abierto?

 

Parece que se trata de un problema aritmético para niños pequeños. Si el agua que cabe un vaso tarda en salir 1/2 minuto, los 30 vasos que caben en el recipiente tardarán en salir 15 mi­nutos.

 

Pero si ustedes hacen este experimento verán que el recipien­te no tarda en vaciarse un cuarto de hora, sino media hora.

 

¿Qué ocurre?

El cálculo que hemos hecho es fácil pero erróneo. El agua no sale con la misma velocidad desde el principio hasta el fin. Des­pués de salir el primer vaso, el chorro de agua tendrá ya menos presión, puesto que el nivel dentro del recipiente habrá bajado, por lo tanto, el segundo vaso tardará más de medio minuto en llenarse. El tercero saldrá aún más despacio y así sucesiva­mente.

 

La velocidad con que un líquido sale por el orificio de un re­cipiente abierto depende directamente de la altura de la colum­na de agua que hay sobre dicho orificio. El genial Torricelli, dis­cípulo de Galileo, fue el primero que estableció esta dependencia expresándola con la sencilla fórmula siguiente:

 

,

 

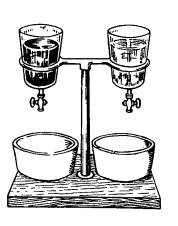
Fig. 58. ¿Qué recipiente se vaciará antes, el que tiene mercurio o el que tiene alcohol? El nivel de los líqui­dos es igual en los dos recipientes.

 

donde v es la velocidad de salida, g la acelera­ción de la gravedad y h la altura del nivel del lí­quido sobre el orificio. De esta fórmula se dedu­ce que la velocidad con que sale el chorro no de­pende en absoluto de la densidad del líquido, es decir, el alcohol, a pesar de ser ligero, y el mer­curio, a pesar de ser tan pesado, saldrán a la misma velocidad si están a un mismo nivel (fig. 58). Según esta fórmula, en la Luna, donde la gravedad es seis veces menor que en la Tierra, el vaso del problema anterior tardaría en llenarse dos veces y media más que en nuestro pla­neta.

Pero volvamos a nuestro problema. Si después de haber sali­do del recipiente 20 vasos de agua el nivel de ésta en aquél (a partir del orificio del grifo) ha bajado hasta la cuarta parte, el vaso 21° se llenará dos veces más despacio que el 19. Y si des­pués desciende el nivel hasta la novena parte, los últimos vaso tardarán tres veces más tiempo en llenarse que el primero. Cuan­do el recipiente está casi vacío el agua sale muy despacio. Resol­viendo este problema por los procedimientos que se estudian en matemáticas superiores se puede demostrar que el tiempo que tarda el recipiente en vaciarse por completo es el doble del que tardaría en salir la misma cantidad de líquido si el nivel inicial permaneciera constante.

 

EL PROBLEMA DEL DEPOSITO

 

Desde lo que acabamos de decir no hay más que un paso a los famosos problemas de los depósitos de los cuales no prescinde ni un solo libro de aritmética o de álgebra. Todos recordamos los clásicos y aburridos problemas escolásticos del tipo que sigue:

 

"Un depósito tiene dos tuberías, una de entrada y otra de salida. El agua que entra por la primera, estando la segunda ce­rrada, puede llenar el depósito en cinco horas. Cuando se abre so­lamente la segunda el depósito se vacía en 10 horas. ¿Cuántas horas tardará en llenarse el depósito si se abren las dos tuberías a la vez?"

 

Hace cerca de 20 siglos que se conocen los problemas de este tipo, es decir, desde la época de Herón de Alejandría. Uno de los problemas de Herón, no tan difícil como sus sucesores, es el si­guiente:

 

Tenemos cuatro fuentes y un depósito grande. La primera en un día lo pone rebosante. La segunda tarda dos en hacer lo que aquélla Y la tercera, en tres, no será menor que ellas. (Para igualarlas, cuatro necesita la cuarta). ¿Qué tiempo tardará el depósito en llenarse, Si se abren las cuatro fuentes en el mismo instante?

 

Hace dos mil años que se resuelven problemas sobre depósi­tos y, tanta es la fuerza de la rutina, que llevamos dos mil años resolviéndolos mal. ¿Por qué? Ustedes mismos lo comprenderán después de lo que acabamos de decir en el artículo anterior so­bre la salida del agua. ¿Cómo se enseña a resolver los problemas de los depósitos? El problema que mencionamos más arriba co­mo típico, por ejemplo, se suele resolver así: la primera tubería llena en 1 hora 1/5 de depósito; la segunda, en este mismo tiem­po, vacía 1/10 del mismo; por consiguiente, cuando están abiertas las dos el agua del depósito aumentará en 1 hora 1/5 – 1/10 = 1/10, de donde resulta que para que llene el depósito por completo ha­cen falta 10 horas. Pero este razonamiento es falso, porque si la entrada de agua se puede considerar que ocurre a presión cons­tante y, por consiguiente, de manera uniforme, con la salida no se puede hacer lo mismo, puesto que se realiza mientras varía el nivel del agua en el depósito y, por lo tanto, de manera no uniforme. Por medio de la segunda tubería el depósito se vacía en 10 horas, pero de este hecho no se puede sacar la conclusión de que por este tubo sale 1/10 parte del agua del depósito cada hora. Como vemos el procedimiento que se sigue en las escuelas es erróneo. Estos problemas no se pueden resolver correctamente valiéndose de las matemáticas elementa­les, por lo tanto, los problemas sobre depósitos (con salida de agua) deben ser excluidos de los libros de problemas de aritmética*.

 

* El lector puede encontrar un análisis detallado de este tipo de problemas en mi libro "¿Sabe usted Física?"

 

 

Fig. 59. El problema del depósito.

 

 

 

 

Fig. 61. Experimento con los "hemisferios de Magdeburgo". Ilustración del libro de Otto Von Gueriche.

 

 

 

 

 

UN RECIPIENTE EXTRAORDINARIO

 

¿Se puede construir un recipiente del cual siempre salga el agua en chorro uniforme, es decir, sin que su corriente pierda ve­locidad, a pesar de que el nivel del líquido descienda? Después de lo que hemos dicho en los artículos anteriores pensarán uste­des que este problema no tiene solución.

 

Sin embargo se trata de una cosa perfectamente realizable. El frasco representado en la fig. 60 tiene precisamente esta ex­traordinaria propiedad. Como puede verse es un frasco ordinario de gollete estrecho, provisto de un tapón atravesado por un tubo de vidrio. Si abrimos el grifo C, que está más bajo que el extre­mo del tubo, el líquido saldrá por él en chorro uniforme hasta que el nivel del agua dentro del frasco llegue a estar más bajo que el extremo inferior del tubo. Si bajamos el tubo hasta que su ex­tremo se encuentre cerca del nivel del grifo, podemos conseguir que todo el líquido que se halle por encima del nivel de su agu­jero salga uniformemente, aunque el chorro sea débil.

 

¿Por qué ocurre esto? Para comprenderlo examinemos men­talmente lo que pasa en el recipiente cuando se abre el grifo C (fig. 60). A1 salir el agua su nivel va bajando dentro del frasco. Esto hace que el aire que hay en la parte superior se enrarezca. Pero entonces, a través del tubo de vidrio, y pasando por debajo del agua, penetra aire del exterior. Este aire forma burbujas al infiltrarse a través del agua y después se acumula sobre ella en la parte superior del frasco. En este caso la presión es igual a la atmosférica hasta llegar al nivel B. Por lo tanto el agua sale por el grifo C impulsada por la presión que ejerce la capa de agua BC, puesto que la presión atmosférica se equilibra dentro y fue­ra del frasco. Y como el espesor de la capa BC permanece constante, no tiene nada de particular que el chorro corra siempre con la misma velocidad.

Pero ahora se nos plantea una nueva pregun­ta: ¿cómo saldrá el agua si quitamos el tapón B, que se encuentra al nivel del extremo del tubo?

 

No saldrá en absoluto (se entiende que esto ocurrirá si el orificio es tan pequeño que su

 

Fig. 60. Esquema del frasco de Ma­riotte. El agua sale del orificio uniformemente.

 

anchura se puede despreciar; de lo contrario el agua saldrá por él presionada por una delgada capa de líquido cuyo espesor será igual a la anchura del agujero). Esto se explica, porque en este caso la presión interna y la externa serán iguales a la atmosférica y, por consiguiente, no habrá nada que estimule la salida del agua.

 

Y si quitamos el tapón A, que está más arriba del extremo inferior del tubo, no sólo no saldrá agua del frasco, sino que en­trará en él aire del exterior. ¿Por qué? Par una razón muy sen­cilla, porque en esta parte del frasco la presión del aire interior es menor que la de la atmósfera exterior.

 

Este recipiente, de propiedades tan interesantes, fue ideado por el notable físico francés Edmond Mariotte y se conoce con el nombre de "frasco de Mariotte".

 

UNA CARGA DE AIRE

 

A mediados del siglo XVII los habitantes de Regensburg y los poderosos príncipes de Alemania, encabezados por su empe­rador, llegados a esta ciudad, fueron testigos de un espectáculo extraordinario: 16 caballos, tirando con todas sus fuerzas, in­tentaron inútilmente separar dos semiesferas de cobre unidas entre sí por simple contacto. ¿Qué unía entre sí a estas dos se­miesferas? "Nada", el aire. Y no obstante, ocho caballos tirando hacia un lado y ocho tirando hacia otro no pudieran separarlas. De esta forma el burgomaestre Otto Von Guericke demostró públicamente que el aire es algo que tiene peso y que presiona con bastante fuerza sobre todos los objetos que hay en la Tierra.

 

Este experimento fue realizado con toda solemnidad el día 8 de mayo de 1654. El sabio burgomaestre supo interesar a todo el mundo con sus investigaciones científicas, a pesar de que esto ocurría en una época en que los desbarajustes políticos y las guerras asoladoras estaban en su apogeo.

 

En los libros elementales de Física figura la descripción del famoso experimento de los "hemisferios de Magdeburgo". No obstante, estoy seguro de que el lector escuchará con gusto esta descripción hecha por el propio Guericke, e1 "Galileo alemán", como llaman a veces a este célebre físico. El libro, bastante voluminoso, en que se describe la larga serie de sus experimentos apareció en Amsterdam el año 1672; estaba escrito en latín y como los demás libros de esta época tenía un título muy largo, que hemos creído interesante reproducir.

 

El capítulo XXIII está dedicado al experimento que nos interesa. A continuación incluimos su traducción literal.

 

"Experimento para demostrar que la presión del aire une dos hemisferios tan fuertemente que 16 caballos no pueden sepa­rarlos".

 

"Encargué dos hemisferios de cobre de tres cuartos de codo de Magdeburgo de diámetro*. Pero en realidad sus diámetros midieron solamente 67/100 de codo, ya que los maestros, como de ordinario, no pudieron hacer exactamente lo que era necesa­rio. Ambos hemisferios se correspondían bien entre sí. Uno de ellos tenía una llave que permitía extraer el aire interior y evi­taba la entrada del aire exterior. Los hemisferios tenían además cuatro argollas, por las cuales pasaban los cordeles que se suje­taban a los atalajes de los caballos. También hice que cosieran un anillo de cuero; este anillo, impregnado en una mezcla de cera y aguarrás y cogido entre los dos hemisferios no dejaba que el aire entrase en ellos. En la llave se enchufó el tubo de la máquina neumática y se extrajo el aire de dentro de la esfera. Entonces se puso de manifiesto la fuerza con que ambas esferas se apretaban entre sí a través del anillo de cuero. La presión del aire exterior las apretaba con tal fuerza, que 16 caballos (de un tirón) no las podían separar o lo conseguían con dificultad. Cuando los hemisferios, cediendo a la fuerza de los caballos, se separaban, producían un estampido como un cañonazo.

 

Pero si se abría la llave y se dejaba entrar el aire, los hemis­ferios se podían separar fácilmente con las manos".

 

Un cálculo sencillo puede aclararnos por qué hace falta tan­ta fuerza (8 caballos por cada lado) para separar las dos partes de la esfera vacía. El aire ejerce una presión aproximada de I kg por cada cm². La superficie del círculo** que tiene 0,67 codos (37 cm) de diámetro será igual a 1060 cm². Por lo tanto, la presión de la atmósfera sobre cada hemisferio será mayor de 1000 kg (1 t). Cada uno de los tiros de 8 caballos tenía, pues, que tirar con una fuerza de una tonelada para poder contrarres­tar la presión del aire exterior.

 

* El "codo de Magdeburgo" mide 550 mm.

** Se toma la superficie del círculo u no la de la semiesfera, porque la presión atmosférica tiene el valor que hemos indicado cuando actúa sobre la superficie formando un ángulo recto con ella. Si la superficie está incli­nada, la presión es menor. En nuestro caso tomamos la proyección rectangular de la superficie esférica sobre el plano, es decir, la superficie del círculo.

 

Parece que para 8 caballos (por cada lado) esto no es mu­cha carga. Pero no hay que olvidarse de que cuando un caballo tira de un carro cargado con 1 t la fuerza que hace no es de 1 t, sino mucho menor; exactamente la que se necesita para vencer el rozamiento de las ruedas sobre sus ejes .y sobre el pavimento. Esta fuerza representa (en una carretera, por ejemplo) el cinco por ciento de la carga, es decir, si el carro pesa una tonelada la fuerza necesaria para arrastrarlo es igual a 50 kg. (Sin hablar ya de que la experiencia demuestra que cuando se enganchan 8 caballos juntos se pierde el 50% del esfuerzo). Por consiguiente, la tracción de 1 t corresponde para los 8 caballos a arrastrar un carro que pese 20 t. Esta es la carga de aire que tenían que arrastrar los caballos del burgomaestre de Magdeburgo. Este esfuerzo se puede comparar con el necesario para mover de su sitio a una locomotora no muy grande, pero que no esté sobre los raíles.

 

Se ha medido que un caballo fuerte tira de la carga con una fuerza total de 80 kg*. Por consiguiente, para separar los hemis­ferios de Magdeburgo, con tracción uniforme, hubieran sido ne­cesarios caballos por cada lado**

 

 

* A una velocidad de 4 km por hora. Se considera que, por término medio, la fuerza de tracción de un caballo es aproximadamente igual al 15% de su peso. Un caballo ligero pesa 400 kg, uno pesado, 750 kg. Durante poco tiempo (el esfuerzo inicial) la fuerza de tracción puede ser varias ve­ces mayor.

** La explicación de por qué hacen falta 13 caballos por cada lado puede encontrarse en mi libro "Mecánica Recreativa".

 

 

 

 

 

 

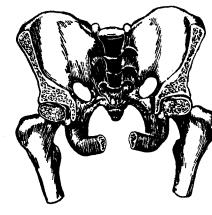
Fig. 62. Los huesos de nuestras arti­culaciones coxofemorales no se sepa­ran debido a la presión atmosférica, que los sujeta lo mismo que a los hemisferios de Magdeburgo.

 

 

 

 

 

 

El lector quizá se asombre al saber que algunas articulaciones de nuestro esqueleto se mantienen unidas por la misma causa que los hemisferios de Magdeburgo. Nuestra articulación coxofemoral tiene unas propiedades parecidas a los antedichos hemisferios. A esta articu­lación se le pueden quitar todos los ligamentos muscu­lares y cartilaginosos sin que se desarticule. Ocurre esto porque la presión atmosférica aprieta entre sí los huesos que forman esta articulación, puesto que en el espacio comprendido entre ellos no hay aire.

 

VASIJAS DE PEGA

 

En los siglos XVII y XVIII los grandes señores se distraían con juguetes como el siguiente: mandaban a hacer un jarro que en la parte superior tenía unos adornos calados bastante gran­des (fig. 66). Este jarro lleno de vino se lo ofrecían a alguien de quien se podían burlar sin temor a las represalias. ¿Cómo beber?

 

 

 

 

 

 

 

 

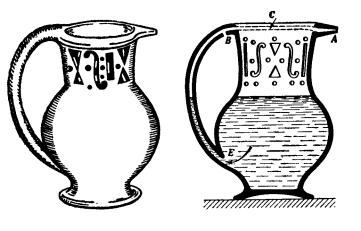
Fig. 66. Vasija de pega de fi­nales del siglo XVIII y corte de la misma en que se ve el ca­nal secreto.

 

 

 

 

 

 

Si empinas el jarro, se derrama el vino por las ranuras caladas sin que ni una gota llegue a la boca. Pasa como en el cuento:

 

Miel y cerveza bebí

y ni el bigote humedecí.

 

Pero el que sabía el secreto de estos jarros, que puede verse en la fig. 66 a la derecha, tapaba con un dedo el orificio B, co­gía entre los labios el pitorro A y chupaba como si fuera de un biberón, sin torcer el jarro. El vino entraba por el agujero E, subía por el canalito que tenía dentro el asa, pasaba después por el borde hueco c y salía por el pitorro.

 

Los alfareros rusos hasta hace poco hacían jarros parecidos a éstos. Yo he tenido ocasión de ver uno en una casa. El secreto estaba muy bien disimulado. El jarro tenía una inscripción que decía: "Bebe pero no te mojes".

 

¿CUANTO PESA EL AGUA QUE HAY EN UN VASO BOCA ABAJO?

 

‑ Nada, claro está ‑ dirán ustedes ‑, ¿cómo va a pesar sí se derrama?

‑ ¿Y si no se derrama? ‑ pregunto yo.

 

En realidad se puede conseguir que el agua no se salga de un vaso boca abajo, es decir, que no se derrame. Este caso es el que se representa en la fig. 67. Como puede verse, una copa de vidrio invertida está sujeta por el pie al platillo de una balanza. La copa está llena de agua, que no se derrama porque los bordes de la copa están sumergidos en el agua que hay en otra vasija. En el otro platillo de la balanza se encuentra otra copa exactamente igual que la pri­mera.

 

¿Hacia qué lado se inclinará la ba­lanza?

Hacia el lado de la copa invertida llena de agua. Esta copa está sometida por arriba a la presión total de la at­mósfera, mientras que por abajo el peso del agua que hay en ella debilita esta misma presión atmosféri­ca. Para restablecer el equilibrio sería necesario llenar de agua la copa del otro platillo.

 

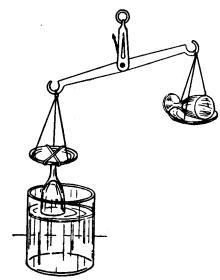
Fig. 67. Procedimiento para pesar el agua que hay en una copa invertida.

 

Por consiguiente, en estas condiciones el agua contenida en un vaso boca abajo pesa lo mismo que la contenida en un vaso en posición normal.

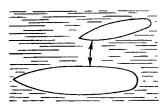
Fig. 68. Posición de los buques "Olympic" y "Hauk" antes del abor­daje.

 

 

 

 

¿POR QUE SE ATRAEN LOS BARCOS?

 

En otoño del año 1912 ocurrió con el "Olympic", uno de los buques más grandes del mundo en aquella época, el caso siguien­te. El "Olympic" navegaba en mar abierto y con rumbo casi paralelo a él y a la distancia de unos cien metros pasaba a gran velocidad otro buque, bastante más pequeño, el crucero acoraza­do "Hauk". Cuando ambos buques ocupaban la posición que representa la fig. 68, ocurrió algo imprevisto. El barco menor torció rápidamente su rumbo y, como si estuviera sometido a una fuerza invisible, puso proa al "Olympic" sin obedecer al ti­món, y avanzó hacia él casi directamente. Se produjo un abor­daje. La proa del "Hauk" se hundió en el costado del "Olympic". El golpe fue tan fuerte que en la banda del "Olympic" se produjo una gran vía de agua.

 

Cuando este caso tan singular fue examinado por el tribunal marítimo, este último reconoció culpable al capitán del "Olym­pic", puesto que, como decía la sentencia, no dio ninguna orden para dejar paso libre al "Hauk", que iba a cruzarse con él.

 

El tribunal de justicia no vio aquí nada extraordinario. Con­sideró que se trataba de una simple negligencia del capitán. Sin embargo, el abordaje fue debido a una circunstancia imprevista, fue un caso de atracción mutua entre dos buques en el mar.

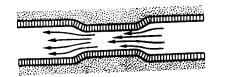Fig. 69. En las partes estrechas del canal el agua fluye más de prisa y presiona menos sobre las paredes que en las partes anchas.

 

 

Estos casos es posible que también ocurrieran antes, cuando los barcos marchaban con rumbos paralelos. Pero hasta que no Se empezaron a construir buques gigantes este fenómeno no se puso de manifiesto con tanta fuerza. Cuando las aguas del océa­no comenzaron a ser surcadas por "ciudades flotantes" el fenómeno de la atracción entre buques se hizo mucho más notorio. Los capitanes de la marina de guerra tienen en cuenta este fe­nómeno cuando maniobran con su buque.

 

Multitud de averías ocurridas en barcos pequeños que nave­gaban cerca de grandes buques de pasajeros o de guerra es po­sible que fueran producidas por esta misma causa.

 

¿Como se explica esta atracción? En primer lugar, esto nada tiene que ver con la ley de la atracción universal de Newton. En el capítulo IV vimos que esta atracción es demasiado pequeña. La causa de este fenómeno es otra muy distinta y se explica por las leyes del movimiento de los líquidos en tubos y canales. Se puede demostrar que si un líquido se mueve por un canal que tiene unos sitios más anchos v otros más estrechos, por los sitios estrechos el líquido pasa más de prisa y presiona menos sobre las paredes del canal que en los sitios anchos, por los cuales pasa más despacio y presiona más sobre las paredes (éste es el llama­do "teorema de Bernoulli".

 

Esto también es justo para con los gases. Cuando se trata de gases este fenómeno se conoce con el nombre de efecto Clément y Desormes (en honor de los físicos que lo descubrieron) y a ve­ces se llama también "paradoja aerodinámica". Este fenómeno fue descubierto casualmente en las siguientes condiciones. En una mina francesa se le ordenó a uno de los obreros que tapara con un escotillón la boca de la galería exterior que servía para suministrar aire comprimido a la mina. El obrero luchó un buen rato con el chorro de aire que entraba en la mina, pero de re­pente el escotillón mismo cerró de golpe la galería, con tanta fuerza, que si hubiera sido más pequeño habría sido arrastrado por la escotilla de ventilación junto con el obrero. El funciona­miento de los pulverizadores se explica precisamente por esta peculiaridad de las corrientes de los gases. Cuando soplamos por el ramal a (fig. 70), que termina en punta, el aire, al llegar al sitio más estrecho, pierde presión. De esta forma, sobre el tubo b se encuentra aire cuya presión es menor que la atmosférica, por lo que esta última hace que el líquido del vaso ascienda por el tubo. Cuando este líquido llega al chorro de aire que sale del tubo a es arrastrado por él y se pulveriza.

 

Ahora podemos comprender cuál es la causa de que los bar­cos se atraigan. Cuando dos buques navegan paralelamente, entre sus costados se forma una

 

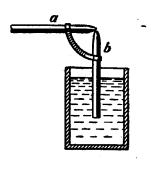
Fig. 70. Esquema del pulverizador

 

 

especie de canal. En los canales ordinarios las paredes están fijas y se mueve el agua; aquí ocu­rre al revés, el agua permanece inmóvil, mientras que las pa­redes se mueven. Pero la acción de las fuerzas no varía por esto. En los sitios más estrechos del canal móvil el agua ejerce menos presión sobre las paredes que en el resto del espacio que rodea a los barcos. En otras palabras, el agua ejerce menos presión so­bre los costados afrontados de los barcos que sobre sus partes exteriores. ¿Qué debe ocurrir entonces? Los buques, sometidos a la presión que el agua ejerce sobre sus costados exteriores de­berán acercarse entre sí y, naturalmente, el barco menor será el que se desvíe más notoriamente, mientras que el de mayor masa permanecerá casi inmóvil. Por esto la atracción se mani­fiesta con más fuerza cuando un barco grande pasa rápidamente junto a otro pequeño.

 

Quedamos, pues, en que la atracción. de los barcos se debe a la acción absorbente de la corriente de agua. Esta misma causa explica el peligro que encierran para los bañistas los rápidos de los ríos y el efecto absorbente de los remolinos de agua. Se pue­de calcular que la corriente de agua de un río cuya velocidad sea de 1 m por segundo arrastra al cuerpo de un hombre con una fuerza de ... i30 kg! Resistirse a esta fuerza no es cosa fácil, so­bre todo en el agua, donde el peso de nuestro cuerpo no nos ayuda a mantener la estabilidad. Finalmente, el arrastre que producen los trenes rápidos sobre los cuerpos próximos también se explica por el teorema de Bernoulli. Un tren que pase con una velocidad de 50 km por hora arrastrará a las personas que estén cerca con una fuerza de 8 kg.

 

            Los fenómenos relacionados con el teorema de Bernoulli no son raros, pero sí poco conocidos por las personas no especiali­zadas en esta materia. Por esto creemos conveniente detener­nos un poco en ellos. A continuación reproducimos un fragmento de un artículo sobre este tema publicado en una revista de di­vulgación científica por el profesor V. Franklin.

 

 

 

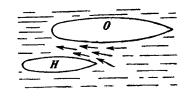
Fig. 71. Corriente de agua entre dos buques que navegan juntos.

 

 

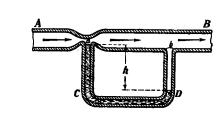
Fig. 72. Ilustración del teorema de Bernoulli. En la parte más estrecha (a) del tubo AB la presión es menor que en la más ancha (b).

 

 

 

TEOREMA DE BERNOULLI Y SUS CONSECUENCIAS

 

El teorema que por primera vez enunció Daniel Bernoulli en el año 1726, dice: en toda corriente de agua o de aire la presión es grande cuando la velocidad es pequeña y, al contrario, la pre­sión es pequeña cuando la velocidad es grande. Existen algunas limitaciones a este teorema, pero aquí no nos detendremos en ellas.

La fig. 72 sirve de ilustración a este teorema.

Por el tubo AB se hace pasar aire. Donde la sección de este tubo es pequeña (corno ocurre en a), la velocidad del aire es grande, y donde la sección del tubo es grande (como en b), la velocidad del aire es pequeña. Si la velocidad es grande, la pre­sión es pequeña, y donde la velocidad es pequeña, la presión es grande. Como la presión del aire en a es pequeña, el líquido se eleva por el tubo C; al mismo tiempo, la gran presión del aire en el punto b hace que el líquido descienda en el tubo D.

 

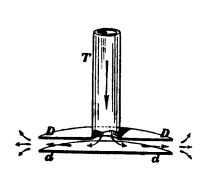
En la fig. 73 el tubo T está soldado al disco DD; cuando este disco se dispone próximo y paralelo a una lámina dd* ligera y libre (por ejemplo, un disco de papel) y se sopla por el tubo T, el aire pasa entre el disco y la lámina a gran velocidad, pero ésta disminuye rápidamente a medida que se aproxima a sus bordes, puesto que la sección de la corriente de aire aumenta muy de prisa y además porque tiene que salvar la inercia del aire que hay en el espacio entre el disco y la lámina. Pero la presión del aire que rodea a la lámina es grande, ya que su ve­locidad es pequeña, mientras que la presión del aire que hay entre ella y el disco es pequeña, puesto que su velocidad es grande. Por lo tanto, el aire que circunda a la lámina ejerce más

 

 

*Este mismo experimento se puede hacer con un carrete de hilo y un circulito de papel. Para que este último no se desvíe hacia un lado, se traspasa con un alfiler, que después se hace entrar en el agujero del carrete

 

 

 

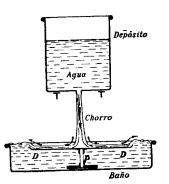Fig. 73. Experimento con discos.

 

 

 

 

 

Fig. 74. El disco DD sube por la barra P cuando sobre él se proyecta el chorro de agua del depósito.

 

 

 

 

 

 

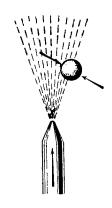
Fig. 75. El chorro de aire no deja que se caiga la pelotita.

 

 

 

 

 

 

 

influencia sobre ella, tendiendo a aproximarla al dis­co, que la corriente de aire que pasa entre los dos, que tiende a separarlos; como resultado la lámina dd se adhiere al disco DD con tanta más fuerza cuanto más intensa sea la corriente de aire que entra por T.

 

La fig. 74 representa un experimento análogo al de la 73, pero con agua. El agua que se mueve rápida­mente sobre el disco DD tiene un nivel más bajo y se eleva ella misma hasta el nivel más alto del agua tranquila del baño, cuando sobrepasa los bordes del disco. Por esto, el agua tranquila que hay debajo del disco se encuentra a mayor prestan que el agua que se mueve sobre él, por consiguiente, el disco se eleva. La varilla P impide que él disco se desvíe lateralmente.

 

En la fig. 75 se representa una pelotita ligera que flota en un chorro de aire. El chorro de aire empuja a la pelotita y al mismo tiempo no deja que se caiga. Cuando la pelotita se sale de la corriente, el aire circundante la hace volver a ella, puesto que la pre­sión de este aire (que tiene poca velocidad) es gran­de, mientras que la del chorro de aire (cuya velocidad es grande) es pequeña.

 

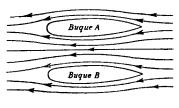            En la fig. 76 pueden verse dos buques que navegan uno al lado del otro en aguas tranquilas; esto es lo mismo que si los dos barcos estuvieran parados y el agua corriese rodeándolos. Entre los buques se estre­cha la corriente y, por lo tanto, la velocidad del agua

 

 

Fig. 76. Dos buques que navegan para­lelamente parece que se atraen entre sí

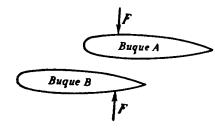
Fig. 77. Cuando los barcos navegan hacia adelante, el B gira y pone proa hacia el A.

 

 

 

 

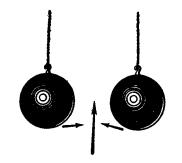
Fig. 78. Si se sopla entre dos esferas ligeras se ve como se aproximan y hasta llegan a juntarse.

 

 

en este sitio es mayor que por los costados exteriores de ambos buques. Por esto, la presión del agua entre los buques es menor que por los otros dos lados y la presión que ejerce el agua circundante (que es mayor) hace que los barcos se aproximen. Los hombres de mar saben perfectamente que los barcos que navegan juntos se at­raen entre sí con bastante fuerza.

El caso en que uno de los buques va detrás del otro, como se representa en la fig. 77, es más peligroso. Las dos fuerzas F y F, que los aproximan entre sí, tienden a hacerlos girar, con la particularidad de que el buque B gira hacia el A con gran fuerza. En este caso el choque es casi inevitable, puesto que el ti­món no tiene tiempo de variar la dirección del movimiento que toma el barco.

 

El fenómeno a que se refiere la fig. 76 se puede demostrar soplando entre dos pelotitas de goma ligeras, colgadas como se ve en la fig. 78. Cuando el aire pasa entre ellas las pelotitas se aproximan y chocan entre sí.

 

¿PARA QUE SIRVE LA VEJIGA NATATORIA DE LOS PECES?

Generalmente, y al parecer con toda verosimilitud, se habla e incluso se escribe que la función de la vejiga natatoria de los peces es la siguiente. Cuando el pez quiere subir desde una capa profunda del agua a otra más superficial, hincha su vejiga na­tatoria; de esta forma el volumen de su cuerpo aumenta, el peso del agua que desaloja se hace mayor que el suyo propio y de acuerdo con la ley de la flotación, el pez se eleva. Cuando no quiere subir más, o quiere descender, el pez hace lo contrario, es decir, comprime su vejiga natatoria. Con esto disminuye su volumen y el peso del agua que desaloja y el pez se va al fondo, de acuerdo con el principio de Arquímedes.

 

Este concepto tan simple de la función que desempeña la ve­jiga natatoria de los peces viene desde los tiempos de los sabios de la Academia de Florencia (siglo XVII) y fue expresado por el profesar Borelli en el año 1675. Durante doscientos años esta hi­pótesis fue admitida sin objeciones y echo raíces en los libros de texto escolares. Pera los trabajos realizados por nuevos investi­gadores han puesto de manifiesto la falsedad de esta teoría.

 

Esta vejiga interviene indudablemente en la natación del pez, puesto que los peces privados artificialmente de este órgano pue­den mantenerse en el agua únicamente a costa de un intenso trabajo con las aletas. En cuanto dejan de mover las aletas se van al fondo. Cuál es, pues, la función de la vejiga natatoria? El papel que desempeña es muy limitado; ayuda al pez a per­manecer a una profundidad determinada, o más concretamente, a la profundidad en que el peso del agua que desaloja su cuerpo es igual al del propio pez. Cuando el pez, moviendo las aletas, baja a una capa inferior a este nivel, su cuerpo experimenta una presión exterior mayor por parte del agua y se contrae compri­miendo la vejiga. De esta forma el peso del agua que desaloja disminuye y resulta menor que el del pez y éste desciende. Cuan­to mayor es la profundidad a que baja el pez, tanto mayor es la presión que sobre él ejerce el agua (esta presión aumenta en I atmósfera cada 10 metros de profundidad), tanto más se compri­me el cuerpo del pez y su descenso se hace más rápido.

 

Lo mismo ocurre, pero en sentido contrario, cuando el pez abandona la capa en que se halla en equilibrio y moviendo sus aletas se eleva a capas superiores. Su cuerpo se libera de una parte de la presión exterior, pero su vejiga, que sigue estando a la misma presión que cuando estaba en equilibrio con la del agua circundante más profunda, hace que se hinche, es decir, que au­mente de volumen y, por consiguiente, se eleva. Cuanto más sube el pez, más se hincha su cuerpo y más rápida se hace la ascen­ción. El pez no puede oponerse a esto "comprimiendo su vejiga natatoria" por la sencilla razón de que las paredes de ésta care­cen de fibras musculares que permitan variar su volumen activa­mente.

 

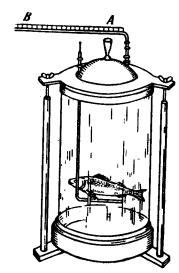El hecho de que el volumen del cuerpo de los peces aumen­te en realidad de una forma pasiva se demuestra con el siguiente experimento (fig. 79). Una breca cloroformada se coloca en una vasija con agua (cerrada) en la que se mantiene una presión semejante a la de la profundidad del agua en que vive el pez en condiciones normales. En la superücie del agua el pez permanecera inmóvil con el vientre hacia arriba. Si hacemos que se sumerja un poco, volverá a subir a la superfi­cie. Cuando lo sumergimos hasta cerca del fondo, se hunde. Pero entre estos dos niveles existe una capa de agua en la cual el pez permanece en equilibrio y ni se hunde ni sale a flote. Esto se comprende fácilmente si recordamos lo que hemos dicho antes, de que fa veji­ga natatoria se hincha y se comprime de forma pasiva.

 

Fig. 79 Experimento con la breca

 

Por lo tanto, a pesar de la idea tan difundida que existe, los peces no pueden voluntariamente hinchar o deshinchar su vejiga natatoria. El volumen de esta vejiga varía pasivamente, es decir, por la acción mayor o menor que sobre ella ejerce la presión exterior (de acuerdo con la ley de Boyle y Mariotte). Estas variaciones de volumen no benefician al pez, al contrario, le perjudican, puesto que hacen que descienda irresistible y aceleradamente hasta el fondo o que ascien­da de la misma forma hasta la superficie. En otras palabras, la vejiga solamente sirve para que el pez conserve el equilibrio cuando está inmóvil, pero este equilibrio es inestable.

 

Este es el verdadero papel de la vejiga natatoria cuando se habla de cómo interviene en la natación. Pero la vejiga realiza además otras funciones en el organismo del pez, aunque cuáles son exactamente estas funciones todavía no está claro, ya que este órgano sigue siendo hasta ahora enigmático. Lo único que se puede considerar completamente esclarecido es su papel hidro­stático.

 

Las observaciones de los pescadores confirman lo que hemos dicho. Cuando pescan un pez a gran profundidad y se les escapa dentro del agua al subirlo, en contra de lo que pudiera esperarse el pez sale rápidamente a la superficie, en vez de volverse a la profundidad de donde lo sacaron. A estos peces les suele asomar la vejiga por la boca.

 

ONDAS Y REMOLINOS

 

Muchos de los fenómenos físicos que vemos a diario no se pueden explicar basándose en las leyes elementales de la Física. Incluso un fenómeno tan corriente como el oleaje del mar en días de viento es inexplicable ateniéndose a los límites del curso escolar de Física. Pero, ¿por qué cuando un barco corta con su proa el agua

 

Fig. 80. Corriente tranquila ("lami­nar") de un líquido por un tubo.

 

tranquila se forman ondas que corren hacia los la­dos? ¿Por qué ondean las banderas cuando hace viento? ¿Por qué la arena de las playas forma ondas? ¿Por qué forma remoli­nos el humo que sale de las chimeneas de las fábricas?

 

Para explicar estos y otros fenómenos semejantes hay que co­nocer lo que se llama movimiento turbulento de los líquidos y de los gases. Aquí procuraremos decir alga de los fenómenos de ca­rácter turbulento y de sus propiedades fundamentales, ya que en los libros de texto de las escuelas apenas si se mencionan.

 

Supongamos que un líquido corre por un tubo. Si al ocurrir esto todas las partículas del líquido se mueven a lo largo del tu­bo formando lineas paralelas tenemos el caso más sencillo de mo­vimiento de un líquido, el flujo tranquilo o como dicen los fí­sicos, "laminar". Pero este no es el caso más frecuente. Al con­trario, lo ordinario es que el líquido corra por el tubo desordena­damente, que forme remolinos que van de las paredes al eje del tubo. Esto es lo que se llama movimiento turbulento. Así es co­mo corre el agua por las túberías de la red de abastecimiento (pero no por los tubos delgados, donde la corriente es laminar). El movimiento turbulento se produce siempre que la velocidad que lleva un líquido determinado al pasar por un tubo (de diá­metro determinado) alcanza cierta magnitud, que se llama velo­cidad crítica*.

 

Los remolinos que forma un líquido transparente al correr por un tubo de vidrio se pueden ver echando en aquél un poco de polvo ligero, por ejemplo, polvos de licopodio. Así se ven per­fectamente cómo los remolinos van desde las paredes al eje del tubo.

 

Esta propiedad del movimiento turbulento se aprovecha en la tecnica en los frigoríficos y refrigeradores. Cuando un líquido circula con movimiento turbulento por un tubo de paredes re

* La velocidad critica de un liquido cualquiera es directamente pro­porcional a su viscosidad e inversamente proporcional a su densidad y al diámetro del tubo por que corre.

 

 

Fig. 81. Corriente "turbulenta" de un líquido por un tubo.

 

 

consecuencia de esto, el ala sufre por abajo un empuje y por arriba una succión (fig. 84). Fenómenos parecidos tienen lugar cuando los pájaros planean con las alas extendidas.

¿Cómo actúa el viento sobre un tejado sometido a él? Los remolinos crean sobre el tejado un enrarecimiento del aire; el aire que hay debajo del tejado tiende a igualar la presión y al subir le empuja desde abajo. Así ocurre lo que a veces tenemos que lamentar; el viento se lleva algún tejado ligero por estar mal sujeto. Por esta misma razón los vidrios de ventana grandes se cimbran hacia afuera cuando hace viento (y no se rompen por la presión exterior).

 

Pero estos fenómenos son más fáciles de explicar por el he­cho de que cuando el aire se mueve, disminuye la presión (véase "Teorema de Bernoulli" pág 124).

 

Cuando una corriente de aire, de temperatura y humedad de­terminadas, se mueve a lo largo de otra corriente de aire, de tem­peratura y humedad distintas, se producen remolinos en las dos. La diversidad de formas que presentan las nubes se debe en gran parte a esta causa.

 

Vemos, pues, que el círculo de los fenómenos relacionados con el movimiento turbulento de los líquidos y los sólidos es muy amplio.

 

VIAJE AL CENTRO DE LA TIERRA

 

Hasta ahora nadie ha penetrado en la Tierra a una profundidad mayor de 3,3 km. El radio de la Tierra tiene 6 400 km. Has­ta el centro de la Tierra queda aún mucho camino que recorrer. Pero la inventiva de Julio Verne hizo penetrar profundamente en las entrañas de la Tierra a dos de sus héroes, el extravagante profesor Lidenbrock y su sobrino Axel. En la novela "Viaje al centro de la Tierra" se describen las extraordinarias aventuras de estos viajeros subterráneos. Entre otras cosas inesperadas con que se encontraron debajo de tierra figura el aumento de la den­sidad del aire. A medida que aumenta la altura el aire se va en­rareciendo con bastante rapidez. Cuando la altura aumenta en progresión aritmética, la densidad disminuye en progresión geométrica. Por el contrario, cuando se desciende más abajo del nivel del mar, el aire sometido a la presión de las capas superio­res debe hacerse cada vez más denso. Los viajeros subterráneos tenían que notar esto forzosamente. A continuación reproducimos una conversación entre el tío‑científico y su sobrino a 12 leguas (48 km) bajo tierra.

“‑ ¿Qué marca el manómetro? ‑ preguntó el tío.

‑ Una presión muy grande.

‑ Ahora comprenderás que bajando poco a poco nos vamos acostumbrando al aire denso y no sentimos molestias.

‑ ¿Y el dolor de oídos?

‑ ¡Tonterías!

‑ Está bien ‑ dije yo, decidido a no contradecir a mi tío ‑. El estar rodeado de aire denso resulta incluso agradable. ¿Se ha dado usted cuenta de lo fuerte que se oyen los sonidos?

‑ Claro. En esta atmósfera hasta los sordos podrían oír.

‑ Pero el aire se irá haciendo cada vez más denso. ¿No al­canzará al fin una densidad como la del agua?

‑‑ Naturalmente. Cuando la presión sea de 770 atmósferas. ‑ ¿Y cuando la profundidad sea mayor?

‑ La densidad también será mayor.

‑ ¿Cómo vamos a descender entonces?

‑ Nos llenaremos los bolsillos de piedras.

‑ Ah, tío, usted siempre encuentra respuesta.

 

No volví a meterme en averiguaciones, porque si no podía pensar cualquier otra dificultad que irritaría a mi tío. Sin em­bargo, me parecía claro que a una presión de varios miles de at­mósferas el aire puede pasar al estado sólido. En estas condi­ciones, aun suponiendo que pudiéramos soportar esta presión, tendríamos que detenernos. Aquí todas las discusiones serían inútiles".

 

LA FANTASIA Y LAS MATEMATICAS

 

Esto es lo que dice el novelista. Pero si comprobamos los he­chos de que se habla en este fragmento resulta otra cosa Para esto no tendremos que bajar al centro de la Tierra. Para nuestra pequeña excursión por el campo de la Física basta tener un lá­piz y una hoja de papel.

 

En primer lugar procuremos determinar a qué profundidad hay que bajar para que la presión atmosférica aumente en una milésima. La presión atmosférica normal es igual a 760 mm de la columna de mercurio. Si estuviéramos sumergidos no en el aire, sino en mercurio, tendríamos que descender nada más que  mm para que la presión aumentase en una milésima. En el aire tendremos que bajar mucho más: tantas veces más como el mercurio es más pesado que el aire, es decir, 10 500 veces. Por lo tanto, para que la presión aumente en una milésima de la normal tendremos que descender no 0,76 mm, como en el mercurio, sino 0,76X 10 500 mm, es decir, cerca de 8 m. Cuando bajemos otros 8 m la presión del aire aumentará en otra milésima de la magnitud anterior, y así sucesivamente*. Cualquiera que sea el nivel a que nos hallemos, en el "techo del mundo" (22 km), en el pico del Everest (9 km) o junto a la superficie del mar, tendre­mos que descender 8 m para que la presión del aire aumente en una milésima de su valor inicial. Por consiguiente, obtenemos la siguiente tabla del aumento de la presión del aire al aumentar la profundidad:

 

La presión al nivel del mar es de 760 mm, igual a la normal.

„      „          a la profundidad de        8 m es   „    „    1,001           de la normal

„      „         „   „         „            „      2X8 m es   „    „   (1,001)²         „    „      „

„      „         „   „         „            „      3X8 m   „   „    „   (1,001)³         „    „      „

„      „         „   „         „            „      4X8 m   „   „    „   (1,001)⁴         „    „      „

En general, a una profundidad de nX8 m la presión atmos­férica será mayor que la normal (1,001)n veces y, mientras la presión no sea demasiado grande, el mismo número de veces aumentará la densidad del aire (por la ley de Mariotte).

Según la novela, en nuestro caso se trata de una profundidad de 48 km bajo tierra, por lo tanto, puede despreciarse la dis­minución de la gravedad y la del peso del aire que ella deter­mina.

Ahora podemos calcular, aproximadamente, la presión que so­portaban los viajeros de Julio Verne a la profundidad de 48 km (48 000 m). En este caso la n de nuestra fórmula será igual a 48000 =6000. Hay, pues, que calcular 1,0016000. Como multipli‑

car 1,001 por sí mismo 6000 veces resultaría aburridillo y nos llevaría mucho tiempo, recurriremos a los logaritmos que, como dijo Laplace, ahorran trabajo y duplican la vida del que calcula**.

* En la siguiente capa de 8 m el aire será más denso que en la anterior y, por lo tanto, el incremento de la presión en magnitud absoluta también será mayor que en la capa anterior. Así es efectivamente, puesto que tomamos la milésima parte de una magnitud mayor.

** Aquellos que al terminar la escuela hayan conservado antipatía por las tablas de logaritmos es posible que varíen este sentimiento hacia ellas cuando conozcan cómo las caracterizaba el gran astrónomo francés en su obra "Exposición del sistema del mundo": `El invento de los logaritmos, al reducir los cálculos de varios meses al trabajo de varios días, es algo que duplica la vida de los astrónomos y los libera del cansancio y de los errores inevitables cuando los cálculos son muy largos. Este descubrimiento es halagúeño para la inteligencia humana, puesto que es totalmente producto de ella. En la técnica el hombre utiliza para aumentar su poder los mate­riales y las fuerzas que le brinda la naturaleza que lo rodea, pero los loga­ritmos son el resultado de su propia inteligencia".

Tomando logaritmos tenemos que el de la incógnita será igual a

6 000 X 1 g 1,001=6 000 X0,00043=2,6.

Por el logaritmo 2,6 hallamos el número buscado. Este nú­mero es el 400.

Así tenemos que a 48 km de profundidad la presión atmosfé­rica es 400 veces mayor que la normal. La densidad del aire so­metido a esta presión, como demuestran los experimentos reali­zados, aumenta 315 veces. Por esto parece un poco extraño que nuestros viajeros subterráneos no sintieran más molestias que "dolor en los oídos". Pero en la novela de Julio Verne se habla de que los hombres pueden llegar a profundidades de 120 y hasta de 325 km. La presión del aire sería entonces monstruosa; mien­tras que la presión máxima que el hombre puede soportar sin perjuicio para su salud es de tres o cuatro atmósferas.

Si por esta misma fórmula quisiéramos calcular a qué pro­fundidad la densidad del aire será igual que la del agua, es de­cir, 770 veces mayor que la normal, obtendríamos la cifra de 53 km. Pero este resultado es falso, ya que a grandes presiones la densidad del gas no es directamente proporcional a la presión. La ley de Mariotte es justa únicamente cuando las presiones no son excesivamente grandes, es decir, cuando no pasan de cente­nares de atmósferas. A continuación damos los datos relativos a la densidad del aire obtenidos experimentalmente:

Presión Densidad 200 atmósferas 190 400 315

600 „ 387

1500 513

1800 540

2100 564

Como puede verse, el aumento de la densidad queda muy re­trasado con respecto al incremento de la presión. En vano el sa­bio de la novela de Julio Verne esperaba poder llegar a una pro‑

fundidad en que el aire fuera más denso que el agua. Esto no lo hubiera podido conseguir nunca, ya que el aire llega a tener la

densidad del agua a la presión de 3 000 atmósferas y después casi no se comprime. En cuanto a solidificar el aire a costa solamente

de la presión, sin enfriarlo intensamente (hasta una temperatura menor de ‑ 146°), ni hablar del asunto.

Pero hay que ser justos y reconocer que cuando Julio Verne publicó su novela aún no se conocían los hechos que acabamos de citar. Esto justifica al autor, aunque no corrija la narración.

Antes de terminar, aprovechemos la fórmula que hemos de­ducido antes para determinar cuál es la profundidad máxima de una mina a la que el hombre pueda descender sin perjuicio para su salud. La presión máxima que puede soportar bien nuestro organismo es de 3 atmósferas. Llamando x a la profundidad de la mina que buscamos, tendremos la ecuación:

x

(1,001)8 =3,

de donde (tomando logaritmos) calculamos x. Obtenemos que x=8,9 kilómetros.

Por lo tanto, el hombre podría encontrarse, sin perjuicio pa­ra su salud, a una profundidad de cerca de 9 km. Si el Océano Pacífico se secara, se podría vivir en casi todas las partes de su fondo*.

EN UNA ,'MINA PROFUNDA

¿Quién ha llegado más cerca del centro de la Tierra? (En rea­

lidad, no en las novelas.) Los mineros, naturalmente. Ya sabe­

mos (véase el cap. IV) que la mina más profunda se encuentra

en Africa del Sur. Su profundidad es mayor de 3 km. Al decir

esto tenemos en cuenta no la penetración de los taladros de per­

foración de pozos, que han alcanzado hasta 7,5 km, sino las pro­

fundidades a que han penetrado los propios hombres. El escritor

francés, doctor Luc Durtain que visitó un pozo de la mina Morro

Velho, cuya profundidad es de cerca de 2 300 m, escribía:

"Los célebres yacimientos auríferos de Morro Velho se encuen­

tran a 400 km de Río de Janeiro. Después de 16 horas de via­

je en tren por sitios montañosos, descendemos a un valle pro­

fundo rodeado por la selva. Una compañía inglesa explota aquí

filones auríferos a una profundidad a la que antes nunca había

descendido el hombre.

El filón va oblicuamente hacia abajo. La mina lo sigue for­

mando seis pisos. Pozos verticales y galerías horizontales. Un

hecho que caracteriza extraordinariamente a la sociedad contem­

poránea es que la mina más profunda que se ha abierto en la

corteza terrestre, el intento más intrépido hecho por el hombre

para penetrar en las entrañas de la Tierra, es para buscar oro

* Las investigaciones llevadas a cabo durante los últimos años han

demostrado que el hombre puede soportar, sin perjuicio para su organismo,

presiones mayores de 30 atmósferas. Esto ha permitido sumergirse en el

136 mar, sin escafandra, hasta profundidades mayores de 300 metros.

Póngase la ropa de trabajo de lona y la cazadora de cuero. Tenga cuidado; cualquier piedrecita que caiga por el pozo puede herirle. Nos va a acompañar uno de los "capitanes" de la mina. Entra usted en la primera galería. Está bien iluminada. Un vien­to helado a 4° le hace temblar; es la ventilación para refrige­rar las profundidades de la mina.

Después de descender en una estrecha jaula metálica por el primer pozo hasta una profundidad de 700 m, llega usted a la segunda galería. Baja usted por el segundo pozo. El aire está caliente. Ya está usted más bajo que el nivel del mar.

A partir del pozo siguiente el aire quema la cara. Sudando a chorros y agachado, porque el techo es bajo, avanza usted en dirección al ruido de las máquinas perforadoras. Envueltos en un polvo denso trabajan unos hombres semidesnudos; el sudor chorrea por sus cuerpos; las botellas de agua pasan de mano en mano. No toque usted los trozos de mineral recién desprendidos, están a 57° de temperatura.

¿Y para qué esta realidad tan espantosa y abominable?

‑ Cerca de 10 kilogramos de oro al día ..."

Al describir las condiciones físicas que existían en el fondo de la mina y el grado de explotación a que estaban sometidos los mineros, el autor francés menciona la alta temperatura pero nada dice de que la presión del aire fuera grande. Calculemos cuál será esta presión a 2 300 m de profundidad. Si la tempe­ratura fuera la misma que en la superficie de la tierra, de acuerdo con la fórmula que conocemos, la densidad del aire aumentaría en

2 300

(1,001) 8 =1,33 veces.

Pero en realidad la temperatura no permanece invariable.

sino que se eleva. Por esto la densidad del aire no aumenta tanto,

sino menos. En definitiva, tenemos que la diferencia entre la pre­

sión del aire en el fondo de la mina y en la superficie de la tierra

no es más que un poco mayor que la que existe entre la del aire

caliente del verano v la del aire frío del invierno. Por esto se

comprende que esta éircunstancia no llamase la atención del vi­

sitante de la mina.

En cambio tiene mucha importancia la notable humedad del

aire a estas mismas profundidades, que hace que la permanencia

en ellas sea insoportable cuando la temperatura es alta. En una

de las minas de Africa del Sur (Johannesburg), de una profundi­

dad de 2553 m, a 50° de temperatura la humedad llega al 100%;

en esta mina se instaló lo que se llama "clima artificial". La ac­

ción refrigerante de esta instalación equivale a 2000 t de hielo. 137