Autor: RAMÓN PERALTA-FABI

EDICIONES
PREFACIO
-
I. INTRODUCCIÓN
II. ¿QUE SON Y CÓMO LOS DESCRIBIMOS?
III .UNA "HISTORIA" DE LAS IDEAS
-
CONSULTA DE LOS OTROS CAPITULOS:

|
Autor: RAMÓN PERALTA-FABI |
 |
|
|
||
 |
||
![]()
Primera edición, 1993
Dibujos: Ramón Peralta Sierra
La Ciencia desde México es proyecto y propiedad del Fondo de Cultura
Económica, al que pertenecen también sus derechos. Se publica con los auspicios
de la Subsecretaría de Educación Superior e Investigación Científica de la
SEP y del Consejo Nacional de Ciencia y Tecnología.
D.R. © 1993 FONDO DE CULTURA ECONÓMICA,
S. A. DE C. V.
Carretera Picacho Ajusco 227; 14200 México, D.F.
ISBN 968-16-4215-5
Impreso en México
![]()
![]()
Este libro fue escrito con la intención de compartir la pasión por entender a los líquidos y gases. Así, aparecen aspectos que finalmente entendemos y otros que siguen escabullendo nuestros afanes cotidianos. Están incluidos algunos temas recurrentes a cualquier nota escrita sobre aguas y vientos y otros un tanto extraños y sorprendentes que forman parte de la misma familia aristocrática de los fluidos. Muchos temas no aparecen debido a varias limitaciones, entre las que se cuentan las del autor, pero que cumplen con el propósito de interesar al lector en buscar lo que no está o en aclarar lo que aquí no se pudo.
Sin desearlo, y en forma casi irremediable, el texto incluye más del autor y de sus intereses que de las exquisitas facetas que presentan los fluidos, tan comunes y especialmente corrientes. La esperanza es que alguna parte de la lectura sea tan agradable como lo fue escribirla y que ninguna sea tan penosa como su redacción.
Agradezco a mi familia y a mis colegas, amigos y estudiantes por las interminables pláticas y sugerencias que sirvieron para mejorar el contenido. En particular, agradezco a Rocío Chicharro y a la correctora de estilo, Laura Pulido, por la lectura y comentarios constructivos que hicieron sobre la versión original; a Ramón Peralta Sierra le debo las ilustraciones, la portada y la pasión por hacer lo que hago.
![]()
LA BELLEZA de un atardecer en el que las nubes se mezclan,
cambian de forma y de color, crecen o se desvanecen hasta quedar en nada, se
multiplica y enriquece al descubrir los diversos y complejos procesos que se
conjugan para presentar el espectáculo. Lo mismo sucede al observar las olas que
llegan a una playa, el fuego en una hoguera o la corriente de un río que,
pareciendo no cambiar y repetirse siempre, nunca son iguales; ésta es parte de
la magia de un fluido. La seducción viene de todas partes: de las gotas de
lluvia que se estrellan en la superficie del agua, de las variadas franjas y
manchas de colores que vemos en una imagen de Júpiter, de las hileras de
pequeñas burbujas ascendentes que parecen salir de ningún lado en el seno de un
vaso de cerveza, del caprichoso ascenso de una columna de humo, de las
maravillosas pompas de jabón y, observando con cuidado, de todo lo que está a
nuestro alrededor. Todas son manifestaciones de lo mismo: la dinámica de un
fluido.
Los fluidos, como genéricamente llamamos a los líquidos y los gases, nos envuelven formando parte esencial de nuestro medio ambiente. El agua y el aire son los más comunes y, como punto de referencia, los mantendremos en mente como prototipos de un fluido. Su ubicuidad les confiere su importancia.
La experiencia humana con los fluidos se remonta más allá de los tiempos históricos. El manejo de los fluidos ha estado íntimamente ligado al desarrollo de la sociedad. No es de sorprender entonces que desde los inicios de la civilización la imagen del Universo incluyera a los fluidos como elementos primarios de su constitución; aire, agua, fuego y tierra son la versión clásica y medieval de gas, líquido, plasma y sólido, o sucintamente, fluidos y sólidos.
Como en la más apasionante novela de misterio, en la que el lector es guiado con información aparentemente disímbola y escasa, los investigadores a través del tiempo han ido recogiendo y organizando datos sobre la naturaleza. La guía es el experimento y la imagen que se va formando, como en un rompecabezas en tres dimensiones, es aún fragmentada; hay ciertas piezas que embonan en grupos y algunos grupos de piezas que se ensamblan entre sí. El caso de los fluidos, que siguen las mismas leyes de la mecánica que rige el movimiento de los cuerpos celestes, es un ejemplo típico. Creemos tener casi todas unas unidas ya entre sí, otras desperdigadas y a la espera de ser probadas. El reto de participar en el juego de comprender y explicar los fenómenos conocidos, predecir nuevos o descubrir otros, sigue abierto. Es un juego colectivo en el que los participantes, que somos todos, heredamos la experiencia de los anteriores y, tras ampliarla, la turnamos a los que siguen aumentando las oportunidades. La solución o soluciones posibles nos eluden hasta ahora, como lo hace el agua con nuestros esfuerzos por retenerla en las manos, escurriéndosenos entre los dedos.
Completar nuestra descripción y comprensión del comportamiento de los fluidos es, además de un fascinante juego, una imperiosa necesidad por manejar nuestro entorno. El aire y el agua son parte esencial de la vida en la forma que la conocemos. El transporte marítimo y aéreo depende de este conocimiento; también la agricultura, que no puede ya lograrse si sólo se depende de un buen clima, sino de sistemas de riego, vastos y eficientes, que permitan optimizar los recursos locales y suplir las deficiencias naturales. La predicción del clima y de sus más violentas manifestaciones, como huracanes y tornados, es mucho más que una curiosidad académica (aunque también lo es). Entender éstos y muchos otros problemas en los que los fluidos participan como protagonistas principales, requiere de una labor creativa y de un trabajo sistemático y sostenido. Los resultados los demanda la sociedad por razones culturales, estéticas y, especialmente, prácticas.
Del inmenso proyecto general de la física nos ocuparemos de la parte que estudia los fluidos desde el punto de vista macroscópico, es decir, como los percibimos en forma más o menos directa a través de nuestros sentidos; la alusión a su estructura atómica será hecha ocasionalmente y en forma lateral. La justificación de esta omisión será discutida más adelante, aunque la conexión entre estos dos aspectos, uno macroscópico y continuo y el otro microscópico y discreto, es de primordial importancia en cuanto al entendimiento último de un fluido. Esta relación es el sujeto de estudio de la teoría cinética y de la mecánica estadística. Dentro del enfoque macroscópico, el de la dinámica de fluidos, consideraremos sólo algunas de las partes del rompecabezas de manera que pueda obtenerse un panorama sobre su comportamiento usual. Si bien es cierto que, dentro de la teoría, los principios generales tienen todos la misma jerarquía, también es cierto que unos son más útiles que otros para entender algunos aspectos de su comportamiento. Este hecho se refleja en las formas y circunstancias en que fueron formulados. Unos fueron intuidos y usados mucho antes de ser explícitamente enunciados. Otros fueron formulados casi en la forma en que los conocemos ahora, sin haberse apreciado su generalidad y sus consecuencias.
Siendo que a través del tiempo, los grandes matemáticos y físicos, salvo raras excepciones, dedicaron parte de su vida a estudiar los fluidos, no deja de sorprender la falta de atención que la historia de la ciencia ha puesto en la génesis y desarrollo de sus brillantes ideas, ingeniosos diseños y espectaculares resultados; una de las excepciones es la excelente obra de Enzo Levi (Levi, 1989). Gracias a los trabajos de aquellos pensadores, a quienes siempre se recuerda con cierta nostalgia, gozamos de una visión panorámica del tema, aprendimos a plantear algunos de los problemas y seguimos explorando los caminos por ellos señalados.
![]()
COMO en casi todas las novelas, todo resulta más comprensible si
se comienza por aclarar de qué se trata, sin echar a perder el final. Así, sería
apropiado que, como con cualquier personaje principal de una novela decente
(cosa que el protagonista no tiene por qué serlo), tratemos de construir su
imagen, esbozar su carácter, describir sus pintorescas reacciones, sus variados
comportamientos y su lenguaje; en fin, de mencionar todos aquellos aspectos que
lo hacen sujeto de escritura y, se esperaría, de lectura.
Como se verá más adelante, el objetivo se logra sólo parcialmente. Resulta que nuestro protagonista no es ni rubio ni moreno, ni alto ni bajo, ni lo uno o lo otro; simple y sencillamente es difícil de acorralar con palabras y escurridizo para manejar. Es más, después de que hablemos de su interesante estructura (digamos, sus raros órganos internos, sus prominentes señas particulares, sus peculiaridades anatómicas y de algunas de sus idiosincrasias y traumas infantiles), resultará que para algunos fines prácticos carece de importancia. Es como si, tras describir minuciosamente el origen de una tormentosa secta a la que pertenece el medio hermano de la heroína, ésta se cambiara de continente y pasara ahí el resto de sus apasionados o bucólicos días, sin relación alguna con los inconfesables crímenes de la susodicha secta. Aun así, un biógrafo meticuloso no dejaría pasar la oportunidad de abordar el mórbido efecto que podría haber causado en su carácter o en sus ocasionales delirios nocturnos.
Advertidos de lo que sigue, mejor es empezar por el principio y entrar en materia, es decir, en fluidos.
II. 1. UNA INDEFINICIÓN PRECISA
La materia, es decir, todo lo que nos rodea y que percibimos a través de los sentidos, viene en tres presentaciones aparentemente distintas y exclusivas: en sólido, en líquido o en gas. Una observación más cuidadosa nos llevaría a pensar que esta clasificación es un tanto simplista y que debiera ampliarse, o cuando menos subdividirse. Así, empezaríamos por organizar las cosas según su textura, color, abundancia, rigidez, etc., hasta llegar al punto en el que cada material quede ubicado y etiquetado correctamente en el nuevo y exhaustivo esquema así elaborado. Este enfoque tendría sus ventajas, pues dada una sustancia con un nombre debidamente asignado (como el piridotín-3-glutaciclina-6-fosfomentasa; le antepongo el artículo "el" porque, de existir, debiera ser masculino), bastaría con buscar en el compendio, por orden alfabético, para encontrar su descripción completa, tal vez una ilustración y las referencias cruzadas a las otras sustancias que comparten una o más características.
En los términos arriba expuestos la tarea parece imposible, si no es que
ridícula. Sin embargo, es ésta una de las formas en que se ha procedido y los
resultados son sorprendentes. Partiendo de la hipótesis, posteriormente
confirmada, de que todo está hecho de un conjunto reducido de elementos básicos
que al combinarse, bajo ciertas reglas y en diversas proporciones, da lugar a la
impresionante variedad que vemos, los investigadores se dieron a la tarea de
aislarlos y caracterizarlos. Ahora contamos ya con obras que resumen el final de
esta tarea monumental, considerada una quimera a mediados del siglo XIX,
que en su forma más sucinta es la tabla periódica de los elementos de
Mendeleev. A pesar de la importancia fundamental de este conocimiento, en cuanto
a nuestra comprensión del Universo se refiere, la clasificación no es suficiente
para deducir las propiedades de los compuestos que estos elementos forman, ni
incluye todo lo que observamos (literalmente, la luz), ni explica cómo un
material dado responde y se comporta cuando permitimos a un agente externo
influir sobre él. Esto último, el comportamiento dinámico de la naturaleza,
exige un tratamiento, un enfoque diferente, más general, universal si es
posible, que permita evitar el estudio detallado de cada material, lo que haría
del programa científico una tarea inaccesible.
Buscando características genéricas, comunes, y las razones para que éstas se manifiesten, llegamos al estudio de la materia en sus diferentes estados de agregación (formas de presentación), que en última instancia hemos reducido a sólidos y fluidos. Parecería ofensivo el tener que explicar lo que es y lo que no es un sólido. Sin embargo, la separación no siempre es evidente, cuando no inadecuada, al presentar un mismo material con facetas que lo identifican como uno y otro, simultáneamente. Por un lado, a casi todos los compuestos los podemos observar en estado gaseoso, líquido o sólido, como al agua; dependiendo de la presión y temperatura a la que se encuentre, será vapor, agua o hielo. Es posible, y el proceso no es nescesariamente complicado, que un gas pueda licuarse sin cambio abrupto en su comportamiento, observándose una formación paulatina en el gas al ir haciéndose cada vez más denso, hasta ser indistinguible de lo que consideramos líquido. Este hecho es el que nos permite tratar a un mismo nivel, con los mismos criterios, es decir, en forma conjunta, a un gas y a un líquido. Esto no sucede en el proceso de la solidificación de un fluido, o el proceso inverso en el que un sólido se licua o evapora. Hay siempre un punto en el que ciertas propiedades cambian radicalmente al aparecer las dos fases: una sólida y otra fluida, cada una con propiedades ópticas, elásticas, etc., muy distintas.
Supóngase que tenemos un medio homogéneo, es decir, un material cuya composición y propiedades son las mismas en cada parte que lo forma. En cuanto al estado físico en el que se encuentra el sentido común (a veces muy poco común) nos dice que si su carácter es etéreo, terso o escurridizo, el medio no es sólido. Si queremos mantenerlo entre las manos y escapa, se trata de un fluido. Si el medio es sólido podemos retenerlo y es posible deformarlo hasta cierto límite. Un fluido parece no presentar límite a las deformaciones que podemos imprimirle. Estas ideas sueltas que forman parte de nuestra experiencia cotidiana son precisamente las bases para definir a un fluido, si delimitamos un poco más los términos y conceptos incluidos. Aún así, veremos que la naturaleza se las ingenia para exhibir ejemplos que escurren por nuestras definiciones sin dejarse atrapar.
"Un fluido es un material que fluye". Así, además de risa, la definición no da más que pena y sorprendería que pudiera servir para caracterizar a una sustancia. Ahora, hay que precisar lo que es fluir. Para esto vamos a separar en dos a las formas en que actúa una fuerza, que tampoco hemos definido, pero que puede entenderse como el efecto de un agente externo; con buena voluntad y sentido común las cosas usualmente funcionan. Toda fuerza (representada por la flecha en la figura II. 1), al actuar sobre una superficie, puede imaginarse formada de dos partes, una normal o perpendicular a la superficie (N) y otra paralela o tangencial a ésta (T). Cada una de éstas, llamadas componentes de la fuerza, tiene un efecto distinto sobre el material. La componente normal es la que asociamos a la presión y tiende a comprimir o estirar, dependiendo de la dirección de la fuerza. La componente tangencial produce un efecto de deslizamiento relativo entre los planos en que imaginamos estructurado al medio y se le llama también fuerza cortante.
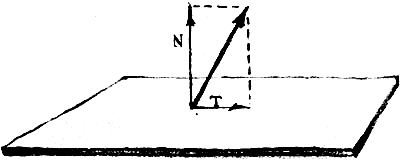
Figura II. 1. Fuerza y su descomposición en componentes normal (N) y tangencial (T).
Para ilustrar esta descomposición de las direcciones y efectos de una fuerza consideremos el siguiente ejemplo. Imaginemos una esponja, de forma regular y pegada a dos vidrios planos en sus caras superior e inferior (Figura II. 2(a)). Si aplicamos una fuerza puramente normal a cada uno de los vidrios (Figura II. 2(b)), la esponja se comprime, reduciendo su volumen pero manteniendo su forma. Si ahora jalamos cada vidrio en dirección opuesta, de modo que la separación entre ellos se mantenga constante, dando lugar a una fuerza de corte sobre la esponja, ésta se deformará manteniendo su volumen (Figura II. 2(c)). Por lo general, una fuerza con una dirección arbitraria produce una mezcla de ambos efectos, dependiendo de la proporción entre su componente normal y su componente tangencial.
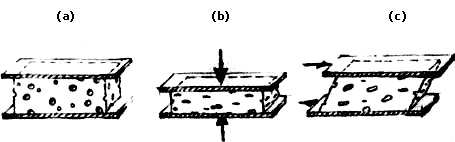
Figura II. 2. Esponja (a), fuerzas normales (b) y de corte (c).
Volviendo a nuestro problema original, consideremos un medio sujeto a fuerzas cortantes, como la esponja en el caso (c). Un material que es sólido se deforma hasta cierto límite, rearreglando sus elementos estructurales (átomos) hasta generar una fuerza igual en magnitud, opuesta en dirección a la aplicada, y así quedar en equilibrio; en última instancia, los átomos ligados entre sí por fuerzas de origen electromagnético se ven obligados a cambiar sus posiciones relativas hasta balancear exactamente la fuerza aplicada. La deformación se detiene en el preciso momento en que esto se logra. Decimos que un material es elástico si al retirar las fuerzas aplicadas recupera su forma inicial. Le llamamos plástico si no recupera su estado original y guarda cierta memoria de las fuerzas que sufrió. Una sustancia que bajo la acción de una fuerza cortante, por pequeña que ésta sea, se deforma sin límite se dice que fluye. ¡Un fluido es un material que fluye! Ahora ya no parece tan tautológica la definición. Así, el mar bajo la acción del viento, que produce una fuerza cortante sobre su superficie, se deforma sin límite, se mueve continuamente sin lograr frenar al viento por tenue que éste sea: la deformación resultante es la que percibimos como oleaje, hipnotizando a unos y mareando a otros.
Parecería que con esto se ha logrado clasificar a todas las sustancias en dos grandes grupos. Sin embargo no es así, lo cual hace el punto más interesante. Hay sustancias que tienen un comportamiento dual para las que nuestra definición es inadecuada o insuficiente. Es tal la diversidad de sustancias que la tarea de completar y precisar una sola definición es inútil.
A las rarezas las tratamos en forma especial, en subgrupos, según las circunstancias. Materiales tan familiares como el vidrio, la pintura y el pavimento pertenecen a esta clase exótica de materiales. El vidrio, que se comporta como sólido cuando lo estudiamos en un laboratorio (o cuando una pelota de béisbol es bateada en la dirección equivocada y va a dar precisamente a...), resulta ser un fluido cuando los tiempos de observación son suficientemente largos. Se puede ver en los emplomados de las viejas catedrales góticas que la parte inferior es mucho más gruesa que la superior. La razón es que el vidrio ha fluido, por cientos de años bajo la acción de la gravedad.
También hay sustancias que presentan comportamiento simultáneo de fluido y sólido. Su tratamiento requiere de consideraciones particulares que caen en el área conocida como la reología. Materiales de este tipo, con propiedades que genéricamente son llamadas viscoelásticas, son por lo general soluciones con gran cantidad de partículas (polímeros) disueltas en ellas. Casos típicos son las resinas, los plásticos, múltiples derivados del petróleo y diversos tipos de champú (el aire de la ciudad de México parecería un buen candidato).
II. 2. LOS ÁTOMOS Y LA VENTAJA DE IGNORARLOS
La concepción atomística de la naturaleza, según la cual todas las cosas
estan constituidas por elementos indivisibles e inmutables, se remonta al origen
de nuestra civilización. Si bien no es sino hasta el siglo XVII que
esta imagen adquiere carácter científico, al empezar a ser fundamentada en la
experimentación, es notable la semejanza que hay entre las ideas básicas en sus
primeras formas y las que hoy en día tenemos.
En la antigua Grecia es donde aparece no sólo la idea general del atomismo, sino las diversas formas que éste adquiere. La existencia de los átomos y del vacío que los rodea, como una necesidad en la explicación de la constitución del mundo, es planteada por razones filosóficas, manteniendo este carácter hasta el renacimiento europeo.
Demócrito, en el siglo V, a.C., es sin duda el
representante más importante del atomismo griego. Para él, la naturaleza estaba
formada de un número infinito de corpúsculos invisibles por su tamaño, que
diferían entre sí sólo en forma, dimensión y estado de movimiento. Comparte con
Parménides la idea de un Universo cualitativamente inmutable, pero difiere de
éste en cuanto al aspecto cuantitativo, pues atribuye los cambios a la
multiplicidad de maneras en que estos átomos se combinan, manteniendo su
naturaleza. Así, un cambio aparente en calidad podía ser entendido, al menos en
principio, como una variación en la cantidad de átomos que participaban en el
proceso.
En la misma época, Empédocles propone la idea de un Universo formado de cuatro elementos básicos, aire, agua, tierra y fuego, que al mezclarse en distintas proporciones generan la inmensa variedad observada. Este modelo, que domina el panorama a todo lo largo de la Edad Media, sin ser atomista en el sentido estricto, refleja la necesidad de reducir a componentes primitivos a la naturaleza. Estas ideas, compartidas y desarrolladas por Platón un siglo más tarde, y la concepción de su discípulo, Aristóteles, en torno a la desaparición de las partes al formar un todo, impidieron el florecimiento y desarrollo del atomismo en la civilización helénica.
Cuando Tito Lucrecio Caro escribe su poema De rerum natura (Sobre la
naturaleza de las cosas) en el siglo I, a.C., el
atomismo griego es incorporado a la cultura latina, enriquecido en el proceso
por Epicuro, su defensor en el siglo III, a.C. Durante
los siguientes diecisiete siglos, crisol del renacimiento y etapa de gestación
de los principios del conocimiento experimental, las ideas filosóficas sobre
este particular se mantienen casi invariables: la materia no puede ser dividida
sin límite y sus elementos constitutivos primitivos son inmutables, incontables
en número y finitos en su diversidad.
En las décadas alrededor de 1600, mientras Galileo Galilei y Francis Bacon establecen las bases del método científico o experimental, Pierre Gassendi revive el atomismo clásico para una época mas madura. Daniel Sennert y Robert Doyle, aceptando la idea atomista, le dan su verdadera dimensión al buscar su contenido en la experimentación. Así, Boyle logra descartar en forma definitiva el sobresimplificado esquema de los cuatro elementos. Un siglo más tarde, Antoine Laurent de Lavoisier desarrolla la metodología del análisis químico y define en la práctica a los elementos químicos. La generación que le sigue establece los fundamentos de la teoría atómica moderna, con la obra de John Dalton, al identificar elementos químicos con átomos y proponer las formas en que éstos se combinan para formar compuestos.
El atomismo griego, la teoría atómica de Dalton y la idea contemporánea sobre la constitución de la materia, comparten suficientes rasgos como para considerarlos un mismo proceso animal observado en su evolución a través del tiempo; cada etapa muestra los cambios indispensables para alcanzar la madurez. Si bien los átomos, concebidos como constituyentes últimos de la materia, han sido sustituidos por las partículas elementales, como el electrón y el neutrino, se ha mantenido el atomismo que imaginara Demócrito. Por otro lado, se ha perdido el carácter inmutable de aquellos átomos de Lucrecio y de Dalton; los nuevos átomos, en el verdadero sentido etimológico del término, pueden combinarse para disolverse en luz (al reaccionar un electrón con un positrón) o perder su identidad formando un todo (al combinarse un protón, un electrón y un neutrino para formar un neutrón).
Esta búsqueda de la explicación última de la materia en términos de sus componentes más simples ha sido, y es, un esfuerzo por alcanzar uno de los objetivos fundamentales de la física. Creemos tener una idea bastante cercana y correcta sobre estos pequeños bloques universales con los que se construye todo lo que observamos. Otro es el problema de cómo éstos se combinan para formar átomos, éstos a su vez formar moléculas y éstas agruparse para conformar un elote, o un insecto rayado que almacena miel en hexágonos o, lo que resulta más sorprendente, dos mamíferos que se comunican entre sí, uno pinto que ladra, y otro bípedo que lo cuida, circunnavega el planeta y se asombra de todo, hasta de su mismo asombro.
No deja de llamar la atención que lo que damos ya como un hecho, la existencia de los átomos, sea en realidad algo que no se puede intuir fácilmente. Nuestros sentidos son incapaces de percibirlos y lo que nos rodea parece consistir de objetos, sólidos y fluidos, de aspecto terso y continuo. Es difícil imaginar que el humo de un cigarro esté formado de moléculas relativamente complejas o que al aire que respiramos lo componen moléculas simples separadas unas de otras millares de veces la distancia que caracteriza su tamaño. Para tener una idea de las dimensiones atómicas tendríamos que imaginar todo amplificado, de manera que por ejemplo una manzana fuese del tamaño de la Tierra. ¡Un átomo de la manzana sería entonces del tamaño de una canica! Si toda esta concepción es cierta, y todo parece indicar que así es, la tarea de explicar, por ejemplo, el movimiento del agua al salir de un tubo, en términos de átomos, parece equivalente a tratar de construir la Torre de Babel.
El problema de estudiar el movimiento individual de miríadas de partículas para luego predecir su comportamiento conjunto es algo que no tiene que ver con la física; en la práctica el problema no puede ni plantearse, mucho menos resolverse. Sería necesario aplicar las leyes básicas de los átomos, la mecánica cuántica, a cada partícula, y conocer detalladamente todas las fuerzas que actúan sobre cada una, establecer sus posiciones en algún momento y, con las matemáticas usuales, resolver simultáneamente el problema para todas.
En una gota de agua hay 100 000 000 000 000 000 (1017) moléculas de agua aproximadamente, ¡tantas como segundos en la edad estimada del Universo!. Sería ridículo intentar escribir las ecuaciones y patético pensar en resolverlas. Nos tomó siglos pasar de una idea filosófica a una concreta que nos permite explicar suficientes cosas como para que su validez esté, por lo pronto, más allá de toda duda razonable. Ahora resulta que el asunto es tan complicado, que la idea es algo enteramente inútil (al menos para estudiar chorros de agua).
La solución de este problema se encuentra en la complejidad del mismo. Suena paradójico, pero con un ejemplo podemos intuir el argumento que siguieron quienes contribuyeron a esclarecer la solución.
Imaginemos un dado perfecto, cada arista de la misma longitud y cada ángulo de 90º. Supongamos ahora que el dado se encuentra parado sobre un vértice, con el vértice diametralmente opuesto sobre una línea vertical, y que nos preguntamos por la dirección en la que va a caer al soltarlo (Figura II.3). Si el lado es perfectamente simétrico, ¡no cae! Se quedará así mientras no sea perturbado. Una corriente de aire o una vibración, por imperceptibles que sean, harán que caiga el dado.
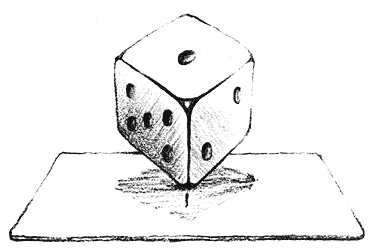
Figura II. 3. Equilibrio de un dado.
Una pequeña variación trae como consecuencia un efecto grande: la caída del dado. Los detalles de la perturbación son casi imposibles de prever y por consiguiente la posición precisa del dado no se puede predecir. Las fuentes que originan estas pequeñas variaciones son diversas, complicadas y difíciles de estimar. Un efecto es siempre el mismo: el dado se cae. Si hacemos una serie de pruebas encontraremos que las direcciones en las que cae están distribuidas sobre un círculo y que las caras que quedan hacia arriba son las tres opuestas al vértice de abajo, apareciendo éstas con igual frecuencia, si el número de pruebas es suficientemente grande. Así, del problema inicial, imposible de resolver, hemos podido encontrar varios aspectos claros y precisos de la solución, quizá obvios o triviales en este caso, pero que nos dicen cosas concretas sobre la caída. En primer lugar sabemos que cae; si esperamos lo suficiente, algo o alguien llegará a importunar la delicada paz del dado. Segundo, el dado no tiene preferencias y cae en cualquier dirección. En tercer lugar, hay tres caras que se reparten por partes iguales el derecho de aparecer arriba.
Este ejemplo ilustra los puntos claves que permiten estudiar la dinámica de un fluido, constituido de un número extraordinario de átomos.
Nuestro sistema, el dado y sus alrededores, todo lo que rodea y afecta al dado, siguen ciertas leyes, las leyes de la mecánica. La aplicación de estas leyes resulta tan complicada que no podemos resolver el problema en la forma originalmente planteada, es decir, predecir en detalle el movimiento del sistema. Si cambiamos el enfoque buscando ahora una descripción cualitativa, más general, es posible entonces responder en forma precisa algunos aspectos de la caída de dados; aspectos de carácter más amplio que no dependen de los minuciosos y abrumadores detalles del proceso. Para esto aceptamos a cambio describir el comportamiento más probable o promedio del sistema, introduciendo un elemento esencialmente nuevo en nuestra descripción: la probabilidad. Esta herramienta, una de las más poderosas que las matemáticas han generado, es ahora un ingrediente fundamental en la física.
Podría pensarse que el precio de nuestra ignorancia o incapacidad es el de conformarse con una descripción más burda, menos exacta, pero no es así. En realidad el problema inicial es irrelevante y en el fondo ni siquiera interesa. Si en el ejemplo del dado pudiésemos resolver un caso en particular, haciendo uso de todo lo que sabemos y una dosis de ingenio, tendríamos precisamente eso, un caso especial. Una pequeña variación y el resultado sería muy distinto (otra dirección y otra cara). Este efecto, en el que un pequeño cambio en el estado inicial produce un resultado final radicalmente distinto, ha introducido más de una sorpresa en nuestro estudio de la naturaleza. Esto es particularmente cierto con los fluidos. Mucho más fructífera ha sido en cambio la búsqueda del comportamiento global, promedio y genérico de un sistema.
No es raro escuchar que cuando se recurre al análisis estadístico o al uso de conceptos probabilísticos es debido a nuestra incapacidad o ignorancia. Sin afirmar que esta posición es ridícula, sí es sólo una parte de la historia; a veces irrelevante. Al promediar muchos detalles se obtiene una descripción completa. En el caso de los gases no es necesario conocer muchos de los detalles atómicos para conocer su temperatura, presión y volumen. Esto es característico del sistema, ¡no de quien lo observa! En todo caso, la tarea del científico es la de explicar cómo y por qué sucede esta maravillosa contracción de la información. Encontrar qué cantidades o propiedades microscópicas son irrelevantes para predecir el comportamiento que observamos es parte de la investigación en curso, si bien contamos con respuestas exquisitas e indicaciones claras de cómo proceder en muchos casos.
La descripción macroscópica de un fluido, es decir, la definición de las cantidades que se usan para caracterizar su estado y las leyes que determinan la variación temporal y espacial de éstas, tiene su fundamento en el comportamiento (dinámica) de las partículas que lo forman. Esto ocurre de tal manera que, al actuar en concierto, cada átomo o molécula pierde su identidad, heredando algunas de sus características a cantidades genéricas o colectivas llamadas coeficientes de transporte, como la viscosidad y la conductividad térmica. Estas etiquetan al fluido, distinguiéndolo de otro de composición diferente.
La teoría que establece la conexión entre este mundo microscópico de átomos y moléculas y el mundo de los fluidos, de chorros y remolinos, es un activo proyecto de investigación en múltiples instituciones académicas en casi todos los países, en particular en México. En el caso de fluidos poco densos, de los gases, la teoría fue construida por James Clerk Maxwell y Ludwig Boltzmann a finales del siglo pasado y desarrollada a todo lo largo del presente siglo; se conoce como la teoría cinética de los gases. El notable éxito logrado en el caso de los gases confirma la viabilidad del programa que busca establecer esta conección en el caso de un fluido arbitrario y fuera de equilibrio.
Desde un punto de vista más práctico, cualquier fluido como el agua o el aire forma una estructura continua y suave al estudiarlo macroscópicamente, es decir en dimensiones mayores a, digamos, décimas de milímetro (0.1 mm = 10-4 m). En un volumen de un cubo de 0.1 mm de longitud por lado, de una millonésima de litro (10-12 m³), hay 7.34 x 1015 (734 seguido de 13 ceros) moléculas de aire, a una temperatura de 27º C ¡y a presión atmosférica! En este volumen, tan pequeño como parece, hay tal cantidad de moléculas que la presencia de unos millones de más o de menos de éstas no afectan de manera apreciable ninguna cantidad medible, aun con los instrumentos más precisos de que se dispone. Estos instrumentos miden cantidades promedio sobre un desorbitado número de partículas, de manera independiente de éste.
En una verdadera escala microscópica los átomos ocupan una fracción muy pequeña del volumen que los contiene, el espacio vacío entre unos y otros ¡es mayor al 99.999... %!, de modo que las propiedades del fluido son muy irregulares, cambiando rápidamente de una región a otra debido al continuo movimiento de las moléculas; no usamos pues esta microescala cuando lo que interesa es entender cómo se vacía un lavabo o se infla un globo.
La hipótesis básica, que es válida para la teoría en todos los niveles, es la llamada hipótesis del continuo. Ésta consiste en suponer que todas las cantidades necesarias para caracterizar a un fluido, como pueden ser su temperatura, su velocidad, su densidad, etc., están bien definidas en cada punto del espacio y varían suavemente de uno a otro, ignorándose así la naturaleza discreta, atómica, del fluido. Por un punto se sobreentiende entonces un volumen muy pequeño, digamos una milésima del considerado en el párrafo anterior, en el que hay un número tan grande de moléculas como para que el promedio de la velocidad no dependa de este número, pero lo suficientemente pequeño como para que pueda verse como un punto por los instrumentos más sensibles y finos.
A partir de ahora dejaremos de lado a los átomos, pues a pesar de su importancia hemos encontrado la ventaja de ignorarlos. Nuestras partículas de fluido tendrán el sentido que dimos a un punto en el fluido. A pesar de la advertencia, volveremos a los átomos en el último capítulo, cuando nos dejemos sorprender por los superfluidos.
II. 3. APEROS: FRASCOS Y TUBOS, IDEAS, MATEMÁTICAS Y... FLUIDOS
El estudio de un fenómeno, o un grupo de ellos, se inicia con una serie de observaciones que permiten apreciar cuáles son los aspectos más importantes, los que gobiernan el proceso. En el fondo, lo que se busca es la forma de simplificar el análisis, aislando las causas que determinan el efecto principal e ignorando aquellas que desempeñan un papel secundario. Establecer cuáles cantidades y la forma en que éstas contribuyen es una parte medular del proceso de entendimiento. Encontrar las razones por las que se combinan de esa manera, usando los principios o leyes correspondientes, es otra etapa igualmente difícil e importante. La última parte, la esencia misma del conocimiento científico, es la predicción. Con base en el estudio previo debe ser posible anticipar el resultado de nuevas observaciones al cambiar de diversas formas el arreglo inicial del fenómeno.
En el esquema anterior está implícito lo que se conoce como método científico. Lejos de ser un procedimiento sistemático y consciente, que lo convertiría en una receta, hermosa, complicada y útil, pero al fin y al cabo una secuencia de pasos bien definidos a seguir, los investigadores intuyen este procedimiento con base en una tradición racional, participando en una o más de estas etapas, omitiendo algunas, ocasionalmente agregando otras y ligados indisolublemente, conscientemente o no, a su entorno social. Lo que sí podemos extraer son algunos de los elementos que parecen siempre estar presentes en una u otra forma en el quehacer científico y en especial en la física; este problema, ciertamente abierto, es materia de la teoría del conocimiento, la epistemología, y ha sido objeto de estudio y reflexión de filósofos e investigadores.
Un primer aspecto es la concepción filosófica que el observador tiene de la naturaleza y del conocimiento que sobre ésta puede adquirir; aquella puede ser explícita o tácita. En este mismo nivel hay una serie de principios filosóficos y de reglas lógicas que el investigador establece, usa y que, normalmente, van implícitas en su trabajo. Así, su contribución diaria puede sobreentender un materialismo que da por hecho la existencia de un mundo objetivo independiente de él, una convicción total en el principio de causalidad que justifica buscar el origen de un efecto, o el uso irrestricto de la lógica clásica, que sin temor al abuso se omiten al discutir de política.
En la parte que toca a las observaciones mismas, empezamos por elaborar un modelo a priori (antes de empezar) sobre el fenómeno al separarlo en partes, el sistema y sus alrededores, y asociarle una regularidad que nos asegure que al repetirse el fenómeno podremos observar y medir lo mismo. Si un resultado no se puede reproducir, por lo general pierde el interés científico, convirtiéndose en un hecho fortuito, objeto de un análisis de otra especie. El llevar a cabo un experimento que "remede en todo" al anterior, tantas veces como sea necesario, es algo que sólo puede lograrse en un laboratorio.
Así, con base en el ingenio, la minuciosidad sistemática, la intuición y la experiencia, como en cada etapa en la dilucidación del fenómeno, se escogen las cantidades relevantes. Acto seguido se determina la forma de medirlas, las posibles fuentes de error y se procede a su cuantificación, estableciendo la consistencia interna y la estadística de los datos obtenidos.
El análisis siguiente consiste en asociar un símbolo a cada cantidad y precisar las posibles relaciones entre éstos, es decir, la forma en que unos dependen de otros. Este proceso lleva a la elaboración de expresiones (fórmulas) que vinculan a los símbolos entre sí, sintetizando grandes cantidades de datos. Las reglas para asociar números a símbolos y para manipular y combinar estos últimos constituye el lenguaje que llamamos matemáticas.
En realidad, las matemáticas son una disciplina teórica que va más allá de un lenguaje o una herramienta, aunque vistas como tales permiten, en manos educadas y hábiles, forjar una imagen abstracta, extremadamente útil y especialmente bella del universo concreto que percibimos. Una virtud de las imágenes así logradas es su capacidad de hablar, a quien las sabe oír, sobre lo que es posible y lo que es probable. ¡Cómo hubiesen aprovechado algo semejante las sacerdotisas del oráculo de Delfos! No siendo de origen divino las predicciones así logradas, como nunca lo fueron las pregonadas por las pitias en Delfos, siempre son sujetas de verificación, a través de más experimentos. Basta con uno de éstos que no corresponda a lo esperado o predicho, para que sea necesario modificar parte de las premisas usadas en la elaboración de la predicción, repitiéndose entonces el proceso. Ha sucedido, por fortuna muy de vez en cuando, que las modificaciones necesarias han ido al mismo fondo de los principios filosóficos.
La física funciona más o menos como lo hemos esbozado. Al construir una teoría se parte de algunos conceptos primitivos que se dejan sin definir o se apela a la intuición para introducirlos, como la masa, el espacio y el tiempo. Después, se definen cuidadosamente cantidades compuestas, como la densidad, la velocidad y la presión, y acto seguido se postulan ciertas proposiciones (basadas en experimentos), los axiomas o leyes fundamentales, como verdaderas y universales. Su inmensa virtud es que, ante la duda, basta con llevar a cabo un experimento para constatar su validez. A partir de los axiomas se deducen entonces una serie de proposiciones o teoremas que, posteriormente, llegan a ser consecuencias no triviales y lejanas de aquellos postulados originales. En muchos casos los teoremas son formulados como conjeturas basadas en la intuición o como resultado de un experimento. El reto en estas circunstancias es encontrar el procedimiento para deducirlo a partir de los axiomas: encontrar la explicación completa del fenómeno a partir de las leyes fundamentales de la teoría.
El estudio de los fluidos, como parte de la física, ha seguido un camino semejante lleno de obstáculos salvados, de anécdotas pintorescas, de errores patéticos, de experimentos notables y de teorías ingenuas. Cada faceta del proceso desempeñó una parte importante para alcanzar el nivel que ahora tiene. En la dinámica de fluidos la dificultad más grande ha radicado en la demostración de los teoremas; una enorme cantidad de resultados experimentales y de fórmulas empíricas esperan ser deducidos de los principios básicos de la teoría. Esto permitiría generalizarlos, arrojando luz sobre otros resultados experimentales aparentemente ajenos e igualmente incomprendidos. No hay ninguna rama de la física que pueda considerarse cerrada y todas son objeto de investigación activa; los fluidos no son una excepción. El problema de la turbulencia, que se menciona más adelante, es uno de los grandes retos de la física teórica.
Para construir un aparato teórico que nos permita entender y explicar el movimiento de los fluidos y de los objetos inmersos en ellos, lo cual observamos todos los días, es necesario introducir tres elementos como punto de partida. El primero es el de los conceptos primitivos de masa, espacio y tiempo, el segundo es el constituido por las cantidades (variables) que usamos para caracterizar y describir a un fluido cualquiera y el tercer elemento es el marco de referencia adecuado para determinar estas variables.
En cuanto a los conceptos básicos las definiciones tal vez dejarán que desear y seguramente el lector podría encontrar otras más adecuadas, pero por ahora no hacen falta. La masa es la cantidad de fluido que medimos con una balanza. El espacio es el escenario que usamos para localizar o ubicar al fluido o a una parte de éste. Imaginamos que existe un punto especial, que llamamos origen, y desde él medimos longitudes con una regla. El tiempo será un parámetro que nos permita ordenar estados diferentes del fluido de acuerdo con su aparición en el experimento; este ordenamiento lo establecemos en relación con el Sol o con un reloj. Si no hay cambios, o estados distintos, el parámetro tiempo desaparecerá de la descripción. Si el fluido presenta comportamiento electromagnético, a los elementos básicos debe agregarse la carga.
El segundo punto es más complicado y tiene que ver con cuántas y cuáles cantidades es necesario disponer para contar con una descripción completa y exhaustiva de un fluido. Esta cuestión, que no está del todo libre de controversia, especialmente cuando se trata de fluidos un tanto exóticos, ha ido resolviéndose a lo largo del tiempo con base en la experiencia. Al quedar enunciadas las leyes en su forma actual se estableció cuántas y cuáles variables, que llamaremos variables dependientes, son las mínimas para caracterizar el estado dinámico de un fluido. Al espacio y al tiempo se les llama variables independientes. Antes de especificar qué variables dependientes se usan para describir a un fluido consideremos ahora el punto que se refiere al marco en el que éstas se definen. Para esto vamos a usar una analogía con la astronomía.
Al observar el cielo en una noche clara, con la ayuda de un telescopio, además de la reverencia que infunde su extensión, profundidad y belleza, aparece la duda por saber en qué dirección fijar el instrumento. Si lo que queremos es llevar a cabo una observación sistemática podríamos escoger entre dos posibilidades: una, enfocar un objeto celeste y seguirlo en su trayectoria. Una vez determinada ésta, repetir el proceso con un segundo objeto y así sucesivamente hasta tener una muestra representativa del movimiento de los objetos más brillantes o más azules o lo que sea; la segunda posibilidad consiste en dejar fijo el telescopio, como una ventana al firmamento, y observar los objetos que cruzan el campo visual, determinando su brillo, color, velocidad o belleza. Posteriormente, cambiar la dirección del telescopio e iniciar de nuevo el proceso y, como en el caso anterior, obtener un muestreo de los objetos celestes y de su comportamiento.
Al primer procedimiento se le conoce como descripción lagrangiana, en memoria de Louis Lagrange, uno de los grandes genios de su tiempo, quien dio a la mecánica de Newton una estructura matemática que lo menos que puede decirse es que su elegante belleza iguala su generalidad. La segunda opción es la descripción euleriana, llamada así en honor a Leonhard Euler, el más prolífico matemático en su época, quien formuló la primera teoría de los fluidos; parte de ella se mantiene en su forma original hasta la fecha.
Estas dos descripciones son usadas en física indistintamente, dependiendo de las circunstancias. Como herramienta conceptual, sin embargo, la formulación euleriana conduce a lo que se llama una teoría de campo, esquema que se emplea en la mayoría de las teorías modernas de la física.
Partir de una descripción lagrangiana supone identificar a una partícula de fluido, considerada como un pequeñísimo volumen, y aplicarle las leyes de la mecánica. Si bien es difícil establecer esta identificación en la práctica, conceptualmente es mucho más atractiva la idea de aplicar los principios de la física a un pedazo de materia que se mueve, manteniendo su identidad como sistema, que aplicarlos a un punto por el que van pasando distintas partes del fluido. En los textos modernos que tratan de este tema se hace precisamente esto; se empieza con una descripción lagrangiana y, una vez introducidos los principios e hipótesis físicas necesarias, se traduce al lenguaje euleriano, usando el diccionario (matemático) apropiado que toda lengua merece.
La formulación euleriana, en la que vamos observando diferentes puntos del espacio y estudiamos lo que ahí sucede al transcurrir el tiempo, da lugar a una teoría de campos. La siguiente idea ilustra el contenido de la frase anterior. En cada punto se hallan definidos ciertos atributos físicos del fluido, digamos densidad y velocidad. De un sitio a otro las propiedades cambian de valor, como en la imagen de un paisaje varían las tonalidades de azul o de verde. Además, con el paso del tiempo las propiedades van cambiando, al igual que sucede en los cambios de las estaciones, cuando una planta nace, crece, florece y muere. Las causas para que cada uno de los cambios se dé pueden ser diversas y lejanas; las apreciamos al estudiar no un sólo punto sino muchos, todos, si es posible.
Finalmente, para concluir con los preparativos que nos permitan entrar en el tema, vamos a introducir las variables dependientes, los campos, que nos facilitan la descripción de diversos procesos y la discusión de los principios subyacentes. Dividimos en dos clases a estas variables, los campos escalares y los campos vectoriales.
Los campos escalares son relativamente sencillos y los conocemos por la práctica que adquirimos al habitar nuestro planeta. Su especificación en cada punto está dada por un número de acuerdo con una escala universalmente aceptada. Una gráfica o una tabla de datos correspondientes cada uno a puntos distintos, nos da toda la información espacial del campo. Si éste cambia con el tiempo se necesita una tabla para cada tiempo. Los campos escalares usuales son la densidad, la temperatura y la presión, que representamos por r, T y p, respectivamente.
La densidad nos da una medida relativa entre masa y volumen, es decir, entre la cantidad de materia y el espacio que ocupa, y es una propiedad más o menos familiar. El oro es más denso que el merengue y éste más denso que el aire, todos lo intuimos.
Es importante hacer notar que la densidad es una propiedad intensiva; es decir, no depende de la cantidad. Por ejemplo, las densidades de un anillo y de un lingote, los dos de plata, son iguales, como lo es su color. Definida como el cociente de la masa, que medimos con una balanza, y el volumen, que medimos con... ingenio, la densidad es una propiedad que no depende de la forma del material, pero sí de la temperatura y la presión (no definidas aún, pero cuyo significado sospechamos). Sus dimensiones son, obviamente, las del cociente masa/volumen. Las unidades correspondientes son, por ejemplo, toneladas/litro, kilogramo/galón, miligramo/kilómetro cúbico, etc. La convención usual es el gramo/centímetro cúbico, gr/cm³ (recordemos que 1 litro = 1 000 cm³ ). La tabla siguiente ilustra los valores de la densidad para algunos objetos.
|
Material
|
Densidad (gr/cm3)
|
|
Hoyo negro
|
~ 1018
|
|
Núcleo atómico
|
~ 1014
|
|
Centro del Sol
|
~ 160 000
|
|
Otro sólido
|
19.3
|
|
Centro de la Tierra
|
~ 12
|
|
Agua
|
1
|
|
Hidrógeno líquido
|
0.07
|
|
Aire ambiente
|
0.0012
|
|
Aire a 300 km de altura
|
~ 10-14
|
|
|
La temperatura, otra noción familiar, es un concepto primitivo que no podemos construir en términos de masa, espacio y tiempo en una teoría macroscópica, pero que está asociado a la idea intuitiva del grado de calentamiento de un cuerpo. Aquí nos contentaremos (indignando quizá a más de uno) con definirla como la propiedad que medimos por medio de un termómetro, instrumento que todos conocemos en alguna versión y que hemos usado alguna vez, posiblemente para evitar ir a la escuela. La escala tiene por unidades a los grados Kelvin (º K) y se conoce como la escala absoluta de temperatura; cada º K es equivalente a un º C. De manera que la escala Celsius, que se usa para asignar temperaturas al consomé de pollo o a un niño resfriado, marca las mismas diferencias de temperatura que la escala absoluta, con la peculiaridad de que la mínima temperatura que es posible alcanzar en la naturaleza es de 0º K (= -273.15º C). En el capítulo VI regresaremos a esta singular ley de la naturaleza.
El otro campo escalar que usaremos es la presión y, como se dijo en la sección II. 1, está definida como la fuerza normal que actúa sobre un área dada. Si la misma fuerza normal actúa sobre dos áreas distintas, la presión es menor sobre el área mayor. Como ilustración imaginemos un objeto cuyo peso es suficiente como para que al ponerlo encima de un huevo éste se aplaste sin remedio. Siempre podemos poner suficientes huevos como para que el peso se reparta entre todos, de modo que la fuerza que recibe cada uno no exceda su "factor de aplastamiento". Al distribuirse la fuerza sobre un área mayor, la presión es menor.
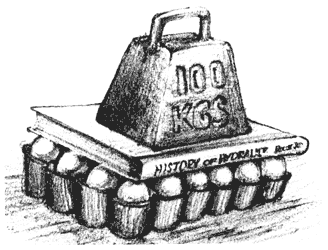
Figura II. 4. Presión: fuerza repartida en un área.
Por eso los cuchillos cortan, los picahielos pican y las palas palean con la eficiencia que lo hacen; ni se diga si además el usuario sabe emplearlos.
Las dimensiones de presión son de fuerza/área y las unidades de mm-Hg); la equivalencia entre éstas es: 1 atm = 760 mmHg = 101,352 Pa. La presión de una atmósfera es igual al peso que una columna de mercurio de 76 cm de altura ejerce sobre un cm², al nivel del mar. Es la misma que ejerce toda la columna de aire arriba de nuestra cabeza. Esto lo demostró Evangelista Torricelli, discípulo predilecto y último de Galileo, usando el sencillo y convincente dispositivo que aparece en la figura II. 5.
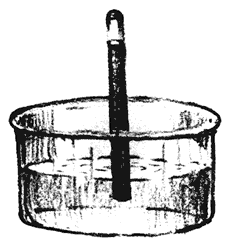
Figura II. 5. Tubo de Torricelli para determinar la presión atmosférica.
Un efecto semejante se observa con el agua, excepto que la columna es ¡de más
de 10 m de altura!; por eso es más sensato usar mercurio, pues siendo metal se
mantiene líquido a temperatura ambiente. Curiosamente, fue René Descartes,
filósofo y matemático del siglo XVII, quien sugirió a Blaise Pascal
el experimento para determinar la forma en que cambia la presión atmosférica con
la altura. El joven genio construyó entonces un barómetro, como el de la figura
II. 5, pero usó vino tinto en lugar del mercurio, ¡en una columna de 14 metros!
Debió ser una experiencia memorable...
En el caso de los campos vectoriales las cosas son un poco más complicadas e interesantes, como las personas. Los vectores requieren para su especificación de algo más que un número: reclaman dirección. La velocidad es un ejemplo característico, ya que no es suficiente dar un número, su magnitud, como 20 km/h; hace falta agregar la información que establece en forma unívoca la dirección en la que se mueve el objeto en cuestión. En cada punto y a cada tiempo es preciso dar tres datos, como por ejemplo la magnitud (el tamaño de a flecha que representa al vector) y dos ángulos.
Convencionalmente se usan los ángulos q y f, definidos geométricamente como se ilustra en la figura II. 6. En ésta, las líneas (ejes) x, y, z son mutuamente perpendiculares y al sistema de coordenadas así definido se le llama cartesiano, en honor a Descartes, a pesar de no haber sido quien lo definió por primera vez.
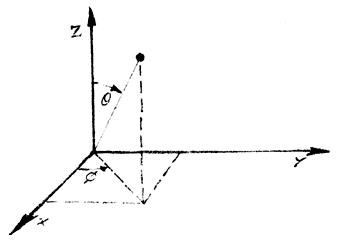
Figura II. 6. Sistema de ejes cartesianos.
Cada vector es entonces representado por una tema de números que nos da, en el punto e instante correspondientes, la magnitud y orientación locales del campo. Una representación frecuente de un campo vectorial es a través de sus línea de campo, que para el caso de la velocidad en un fluido se llaman líneas de corriente o de flujo. En cada punto de éstas el vector velocidad (cada flecha) es tangente. En donde las líneas de corriente tienden a juntarse la velocidad es mayor que en aquellas donde parecen separarse. Si consideramos flujos en dos dimensiones, como el flujo de una película delgada encima de una superficie, sólo necesitamos dos cantidades, la magnitud y el ángulo con respecto a una dirección; esta última la escogemos con base en algún capricho o conveniencia. En la figura II. 7 se ilustran estas curvas.

Figura II. 7. Flujo uniforme y lento alrededor de un cilindro circular. Nótese que es (casi) imposible distinguir la dirección del flujo.
La velocidad, instantánea y local, la definimos como el cociente de la distancia recorrida y el intervalo de tiempo que le toma recorrerla. La velocidad así definida puede cambiar de un punto a otro, o en un mismo punto con el paso del tiempo. Los intervalos de tiempo que corresponderían a esta definición los supondremos tan pequeños como sea posible medirlos en un experimento. En la práctica, lo que se acostumbra hacer es suspender en el fluido partículas reflectoras de luz (hojuelas de aluminio) que al ser iluminadas son captadas por una cámara; la exposición debe ser tan breve como para que las trazas dejadas en la película sean segmentos rectos. El tiempo de exposición es el intervalo de tiempo y la longitud de la traza es la distancia recorrida. La hipótesis implícita es que las partículas suspendidas en el fluido se mueven con éste sin alterar el flujo, de modo que las fotografías nos revelan las líneas de corriente y las velocidades (Figura II. 8).

Figura II. 8. Visualización, por medio de trazadores, de flujo alrededor de un cilindro circular. La velocidad del flujo es mayor que en la figura II. 7.
La fotografía muestra el flujo alrededor de un cilindro, como en la figura anterior; la diferencia estriba en que en este caso la velocidad con la que llega el fluido (de derecha a izquierda) es mucho mayor.
Esta técnica de visualización, introducida a principios de siglo, es hoy en día un elaborado arreglo experimental en el que intervienen todos los adelantos tecnológicos en óptica, electrónica, computación y diseño mecánico. El procesado numérico de imágenes y datos, logrados a partir del análisis de luz láser, dispersada por esferas de poliestireno de una micra de diámetro suspendidas en el fluido, nos permite estudiar minuciosamente flujos que hace unas décadas no se imaginaban, en particular los flujos turbulentos, caóticos y complejos, que discutiremos en el capítulo V.
![]()
![]()
LA FORMA en que fueron descubriéndose efectos, principios y
leyes en muchos casos sólo puede imaginarse, pues existe una laguna en cuanto a
los protagonistas y sus condiciones sociales, económicas y culturales. La
humanidad ha vivido siempre con fluidos. Cómo y cuándo aprendió a usarlos sólo
puede adivinarse. En el presente libro no están todos los que fueron, aunque sí
fueron todos los que están. Muchos nombres, fechas y circunstancias aparecen más
como guía cronológica que como reconocimiento del papel que desempeñaron en la
edificación de la actual teoría de los fluidos.
Una historia no es sólo una secuencia de nombres, fechas, hechos y las anécdotas que los conectan. Es más bien una explicación e interpretación de éstos a partir de hipótesis fundamentadas y basadas en patrones globales del comportamiento; en nuestro caso es la tarea de los profesionales del campo, los historiadores de la ciencia. Más que evocar una historia, lo que haremos será una visita parcial a través del tiempo para recordar pasajes exquisitos del desarrollo del pensamiento humano. Así, pasaremos por algunos aspectos que costaron mucho entender o manejar, por ciertos puntos sencillos y prácticos que nos dejan sospechar las peculiaridades de un fluido y otros más bien curiosos o simplemente divertidos, que aparecen distribuidos en el tiempo y en diferentes sitios, lo cual les da una perspectiva que, al recordar las circunstancias culturales, políticas, sociales o económicas, permite intuir la historia.
No es casual que los cambios y avances importantes que modificaron cualitativamente el conocimiento de la dinámica de los fluidos se llevaran a cabo en forma paralela a los cambios sociales. Es importante subrayar aquí, aun cuando quizá no pueda apreciarse en lo que sigue, que las etapas diversas de organización social, el florecimiento de una cultura o el decaimiento de una civilización, se ven reflejadas en el desarrollo particular de los fluidos. No puede entenderse éste si no es como una huella más de la actividad humana en su conjunto.
III. 1. SOBREVIVENCIA, MAGIA, NECESIDADES Y LUJOS
Hasta hace aproximadamente 100 000 años el hombre seguía tratando de acostumbrarse a vivir bajo los árboles. El paso de recolector de frutos, que afortunadamente no hemos abandonado del todo, al del cazador, fue muy largo y es difícil intuir siquiera cómo se llevó a cabo. En este paso inventó y descubrió múltiples utensilios que le hicieron más fácil su existencia en un medio ajeno y hostil que luego dominó y, diríamos ahora, casi se acabó. Inventó la rueda mucho después del vestido y descubrió el fuego antes que aquélla. Desarrolló armas para subsistir, descubrió después el bronce y, hace unos 10 000 años, la agricultura. Probablemente aprendió a manejar los fluidos en forma circunstancial en este proceso.
Los primeros que se estaban ahogando por humo dentro de una cueva sacaron al fuego a la intemperie o se buscaron una cueva con el techo más alto, y aprendieron que el aire caliente sube, pero sin intuir en ello el principio de la flotación. Los primeros navegantes tal vez surgieron de una poco afortunada pérdida de equilibrio en la orilla de un río y del fortuito paso de un tronco en la vecindad inmediata. También podemos imaginar que, al observar que ciertos objetos flotaban en un río, a más de uno se le ocurrió aprovechar el hecho para viajar río abajo y, con suerte, al otro lado.
La evolución de un tronco a una canoa, de ésta a una balsa y de ésta a un medio de carga y transporte colectivo, así como del mecanismo de propulsión de varas a remos y de éstos a velas, sólo podemos reconstruirlo usando el sentido común y una fértil imaginación. Algo semejante puede decirse de las armas. El proceso que va desde arrojar piedras y palos, que a más de una presa sólo debe haber irritado lo suficiente como para comerse al cándido ancestro, hasta la invención del mazo y, mucho más tarde, hace unos 30 000 años, el arco y la flecha, comprende múltiples pruebas e insólitas experiencias. Bajo la presión de la supervivencia el hombre aguzó el ingenio para adaptarse y manejar su ambiente que, gústele o no, lo dominan los fluidos.
En esta etapa de la protohistoria, que abusivamente catalogamos de supervivencia, se hicieron obras notables destinadas al riego. Las necesidades agrícolas de las culturas que florecieron en Mesopotamia y Egipto, al menos 4000 años a.C., llevaron a diseñar y construir presas y diques, cuyos restos aún pueden apreciarse en las márgenes de los correspondientes ríos. Vestigios semejantes, de tiempos casi tan remotos, fueron descubiertos en las riberas de ríos en la India y la China. La construcción de canales para riego, transporte y surtido de agua a las grandes metrópolis de entonces confirma la relación directa entre el nivel de una civilización y la posesión de una tecnología para mantenerla; en particular, la relación con el agua.
En forma paralela a las obras hidráulicas a gran escala se desarrollaron artefactos, instrumentos y curiosidades asociadas al comportamiento de los fluidos. Es posible suponer que el ser humano intuía algunos principios básicos, si consideramos su notable conocimiento empírico. El uso del fuelle, la jeringa y el sifón era frecuente, como lo reflejan los legados pictóricos y estelas fragmentadas que se conservan, mismas que muestran la existencia de la pipeta, la clepsidra, reloj de agua usado en Babilonia y posteriormente en Egipto, y el uso de los vasos comunicantes. Hubiera sido difícil, muy difícil, llevar a cabo algunas obras de ingeniería sin algunos de estos aparejos. El nivel de pisos y bóvedas seguramente se establecía, como aún hoy lo hacen los buenos albañiles, usando el principio de los vasos comunicantes.
La clepsidra, perfeccionada y usada a través de la Edad Media, consistía en un recipiente con un orificio por el que el agua goteaba a una velocidad constante. El nivel en el recipiente, al ir bajando, marcaba el tiempo en una escala fija en las paredes. Esta idea sencilla, como tantas otras, fue desarrollada hasta alcanzar un alto grado de complejidad técnica y artística.
|
|
Figura III. 1. Vasos comunicantes (a) y clepsidra (b).
El paso de la información en forma oral, de una generación a otra, hizo que gran parte de ella se perdiera en el tiempo. Por otro lado, algunos instrumentos y tal vez sus principios se manejaban con el más meticuloso sigilo por quienes detentaban el poder político o religioso, o ambos, como usualmente sucedía. Los portentos exhibidos en los templos egipcios para mantener la fe, mostrar el beneplácito de los dioses o dejar ver la ira divina, se lograban usando mecanismos hidráulicos ocultos, empleando aire o agua como vehículo; elevar objetos, desplazarlos y, con ingenio, desaparecerlos, fue una práctica desarrollada en ciertas esferas no exclusivas a los cultos a Ra. Que el saber trae consigo el poder no sólo fue explotado por quienes disfrutaban los médanos del Nilo... Pero el secreto que rodeó a esa "tecnología" se quedó en el pasado y no podemos más que especular qué tanto la entendían.
Desde el remoto y oscuro pasado hasta el florecimiento de la cultura helénica, el hombre acumuló un vasto conocimiento práctico sobre el comportamiento de los fluidos. De los complejos sistemas de riego a las elaboradas embarcaciones propulsadas por viento y de las aerodinámicas flechas y lanzas, al sifón y la clepsidra..
Las extensas guerras de conquista de Alejandro Magno permitieron a la civilización occidental enriquecerse con el legado asiático. Alejandría sustituyó a Atenas y amalgamó la cultura de la época, resumiendo el conocimiento previo en su legendaria biblioteca. No es de sorprender que ahí brillaran las artes y ciencias con Euclides, Arquímedes y Ptolomeo, entre otros.
De las diez obras que se conocen de Arquímedes (287-212, a.C.) destacan sus dos volúmenes sobre la hidrostática y la flotación. En la mejor tradición de la escuela de Euclides, con cuyos discípulos se educa, basa todo su análisis en dos postulados sencillos y ciertamente correctos. A partir de éstos demuestra varios resultados que todavía forman parte del cuerpo de los teoremas básicos de la hidrostática y la estabilidad de cuerpos que flotan. Uno de ellos es el principio que lleva su nombre y establece que "si un sólido es parcial o totalmente inmerso en un fluido, sufre una fuerza ascendente igual al peso del fluido desplazado". Este sencillo enunciado nos permite entender un sinnúmero de fenómenos aparentemente disímbolos Veamos ahora tres de ellos: la flotación de un barco, la flotación de globos meteorológicos de altura fija y la proporción de oro en un anillo de bodas.
El principio dice que las cosas flotan en un fluido, lo que implica que pesan menos. La reducción en peso es igual al peso de una cantidad de líquido de volumen igual al del objeto sumergido. Consideremos un ejemplo. Imaginemos un cubo de cuarzo de 1 cm³, se mide un centímetro por lado. Al vacío, encontramos que pesa 2.65 g. Al sumergirlo en agua desplaza 1 cm³ de ésta. Al pesar esta cantidad de agua se halla que pesa 1 g. Por lo tanto, en el agua, el peso de nuestro cubito de cuarzo es de 1.65 g.
¿Por qué flota un barco de acero?
Puesto que un metro cúbico de agua pesa una tonelada, para hacer flotar (reducir su peso a cero) a un barco de 1 000 toneladas es preciso que desplace 1 000 m³ de agua. Es decir que el volumen del barco, abajo de su línea de flotación (Figura III.2), debe ser de, digamos, ¡un cubo de 10 m por lado! Si es más largo que ancho no tiene por qué estar tan sumergido y será de menor calado. Criterios de estabilidad, también desarrollados por Arquímedes, son algunos de los aspectos que determinan la forma más adecuada para el casco del barco, la parte sumergida.

Figura III. 2. Línea de flotación.
¿Cómo subir un globo a una altura predeterminada?
Un globo lleno de algún fluido menos pesado que el aire sufre una fuerza que lo hace ascender, por flotación. Puesto que con la altura el aire es cada vez menos denso, más enrarecido, el globo subirá hasta la altura en que ambos fluidos (el contenido en el globo y el aire externo desplazado) pesen lo mismo. Conociendo la forma en que varía la densidad del aire con la altura es posible predeterminar la altura a la que un globo meteorológico llegará y permanecerá, con sólo variar su volumen y contenido. Estos globos se emplean principalmente para medir propiedades de la atmósfera como la presión, la temperatura, la humedad y los contaminantes (¡en la ciudad de México éstos pueden medirse con un globo sobre la banqueta!).
Siendo el aire un fluido, todas las cosas sufren flotación y, me apena decirlo, ¡las personas son mas pesadas de lo que creen!
Otro ejemplo está conectado a la leyenda según la cual Arquímedes descubrió la flotación. Hierón I, rey de Siracusa (Sicilia), cuna y residencia de Arquímedes, deseaba saber si su corona contenía oro en la proporción adecuada. La solución la encontró Arquímedes, se dice, al entrar en el agua de un baño público, del que salió eufórico gritando "¡eureka!", rumbo a su casa, sin siquiera vestirse. Apenas llegó sumergió en agua pesos de oro y plata iguales, determinando los desplazamientos de agua respectivos. Al comparar éstos con el desplazamiento que generaba la corona determinó el porcentaje de cada metal por medio de una sencilla regla de tres. Con un anillo de bodas el proceso es el mismo, aunque las consecuencias son más difíciles de prever...
El trabajo de Arquímedes en hidrostática es uno de los grandes logros de las matemáticas y mecánica griegas (aunque él era tan griego como un latinoamericano español). "Es uno de los monumentos más espléndidos a su genio [...] al que poco han podido agregar quienes le sucedieron", dijo Lagrange, casi 2 000 años después. Su genio en las matemáticas lo pone en la categoría que solo comparte con Isaac Newton y Friederick Gauss.
La herencia que recibió Grecia para su notable desarrollo en todas las áreas le fue legada principalmente por Mesopotamia y Egipto. Sobre ella construyó el partenón intelectual que conocemos. Por otro lado, las bases sobre las que creció la cultura latina fueron tomadas e incorporadas intactas de los griegos. El imperio romano se consolidó sin que Alejandría hubiese dejado de ser el emporio cultural del mundo occidental. Si Grecia es recordada sobre todo por sus contribuciones en filosofía, artes y matemáticas, Roma buscó brillo en otras direcciones y muy poco contribuyó al avance de las matemáticas y al conocimiento de los fluidos.
Los mil quinientos años subsecuentes fueron ricos en obras de gran importancia en torno al manejo de aguas. Todavía pueden apreciarse los notables acueductos que los romanos sembraron en el orbe que dominaron. El diseño y construcción de sistemas de aprovisionamiento de agua, de su distribución a través de grandes ciudades y de los drenajes correspondientes, hablan del grado de desarrollo de la ingeniería hidráulica en el imperio. La necesidad de resolver problemas prácticos impulsó ese desarrollo. El regado de inmensos jardines palaciegos y el proveer de comodidades a sus ocupantes fue un ingrediente adicional. Poco o nada se logró sobre el entendimiento y uso del agua y el viento. El intercambio con el mundo árabe, a través de las diversas guerras de conquista y reconquista mutua, incluyendo las Cruzadas, permitió un flujo de ideas, invenciones y costumbres que en el crisol del tiempo dieron luz a la deslumbrante explosión renacentista.
III. 2. DE LA METAFÍSICA A LA FÍSICA
Los diez siglos que siguen a la caída del Imperio romano y que gestan la
aparición de una brillante era en la historia de nuestra civilización, sirven
para consolidar el sistema económico feudal y el poder de la iglesia cristiana,
asimilándose el legado filosófico griego. Este último aspecto llegó a su climax
con la aristotelización del cristianismo por Tomás de Aquino en el siglo
XI. La incorporación de las matemáticas, la lógica, la metafísica y
la astronomía griegas a la enseñanza en las "universidades" medievales, que
fundara Carlomagno en el siglo VIII, llevó a la formulación de la
educación escolástica basada en las siete artes liberales agrupadas de la
siguiente manera: el trivium (gramática, lógica y retórica) y el
quadrivium o artes matemáticas (aritmética, astronomía, geometría y música).
En el periodo que concluye con el siglo XIV destacan los
procesos de crítica a la metafísica y mecánica aristotélicas, representados por
Juan Buridan en Francia (1300-1358) y Guillermo de Occam (1285-1349) en
Inglaterra. Esta etapa de revisión crítica fue el fruto de un proceso lento,
laborioso y acumulativo de múltiples, protagonistas, tiempos y lugares. Una
consecuencia directa de esto es el nacimiento de las ciencias experimentales.
En un siglo de notable eslendor sobresale un hombre que se destacó en todas y cada una de las diversas actividades en las que estuvo interesado. Su universalidad sólo es igualada por su profundidad y calidad. Leonardo da Vinci (1452-1519), en cuanto a la ciencia y a los fluidos se refiere, marca el siguiente paso después de Arquímedes.
Como pocos de sus antecesores y contemporáneos, Leonardo subrayó en numerosas ocasiones la necesidad ineludible de la observación y el experimento. Así lo mostró en sus bellos, meticulosos y copiosos dibujos; una exquisita selección puede encontrarse en la publicaci ón del Códice Hammer (Hammer, 1972). Sus razones se pueden leer en algunas de sus notas, por ejemplo: "Huid de la opinión de los especuladores, pues sus argumentos no están sustentados en la experiencia [...] a diferencia de ellos, no puedo citar autoridades, pero, más importante y digno, es argumentar con base en el experimento, maestro de sus maestros." Más tarde, discutiendo su método de trabajo escribió: pero antes llevaré a cabo algunos experimentos, ya que es mi premisa empezar así y entonces demostrar por qué los cuerpos se comportan de cierta manera. Este es el método que debe seguirse en la investigación de los fenómenos naturales [...]".
De la gran cantidad de observaciones y experimentos que llevó a cabo sobre el
comportamiento de los fluidos, Leonardo obtuvo resultados cuantitativos y
generalizaciones sorprendentes que no fueron apreciadas sino mucho después,
¡algunas hasta el siglo XIX!
Encontró que el aire y el agua tienen un apellido común. Al comparar en forma sistemática los movimientos de masas de aire (vientos) y agua (estanques, ríos y mares) intuyó, citándolo en forma recurrente, los elementos comunes de su comportamiento.
Al observar el movimiento de aguas en ductos, canales y ríos, descubrió y formuló en forma cuantitativa uno de los principios fundamentales en la mecánica de los fluidos: el principio de continuidad o de conservación de la masa. Si bien es cierto que al menos desde la época de Arquímedes se sabía que el agua que entra por el extremo de un tubo sale por el otro, la relación entre este hecho y la descarga era si acaso sospechada, aun por los constructores romanos. La descarga es la cantidad de fluido que atraviesa una sección de un tubo o de un canal por unidad de tiempo. Por ejemplo, el número de litros por segundo que pasa por cualquier parte de un tubo, cuya sección sea variable, es siempre el mismo.
En las palabras de Leonardo: "En cada parte de un río, y en tiempos iguales, pasa la misma cantidad de agua, independientemente de su ancho, profundidad, tortuosidad y pendiente. Cada masa de agua con igual área superficial correrá tanto más rápido como poca profunda sea [...]" (ver Figura III. 3);"[...] en A el agua se mueve más rápido que en B, tanto más como la profundidad de A cabe en B...".
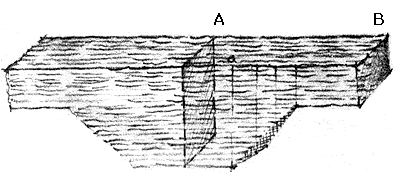
Figura III. 3. Secciones de Leonardo da Vinci.
Este análisis básico y casi evidente, que eludió a sus predecesores, puede considerarse como la primera formulación clara y cuantitativa de la ecuación de continuidad para el flujo estacionario (que no cambia con el tiempo) de un fluido incompresible (de densidad constante). Este resultado, en términos más apropiados, que no más comunes, establece que la velocidad es inversamente proporcional a la sección transversal. Equivalentemente, el producto de la velocidad y el área, en cada sección, es constante. La generalización de este resultado a la forma en que hoy se conoce tomó todavía 300 años mas.
Otros estudios de Leonardo versaron sobre el vuelo, la generación y propagación de ondas, el movimiento de remolinos (vórtices) y el papel de éstos en los flujos complicados e irregulares que llamamos turbulentos. Estos estudios de carácter cualitativo o puramente descriptivo influyeron en forma directa e indirecta en el desarrollo de la hidráulica y la hidrodinámica, entendidas éstas como la parte práctica y teórica de la mecánica de fluidos, respectivamente. La percepción visual de Leonardo fue la herramienta clave de su obra artística y científica, la cual se aprecia en cada detalle de sus penetrantes y hermosas ilustraciones, y gracias a ella estableció una pauta en la búsqueda del conocimiento.
Si la observación y la experimentación, entendidas como el registro meticuloso y pasivo, la primera, y la ocurrencia intencional, repetitiva y controlada del fenómeno, la segunda, son elementos indispensables del conocimiento científico, el uso de un lenguaje adecuado y la generalización deductiva o inductiva las complementan y dan sentido.
A Galileo Galilei (1564-1642) es a quien, un siglo después, le toca completar el esqueleto del método científico, pues transforma a la mecánica en una ciencia partiendo de una crítica constructiva de la metafísica escolástica. Usando a la experimentación como guía, como lo hiciera Leonardo, introduce el lenguaje de las matemáticas para formalizar y extender sus resultados, generalizar sus concepciones y sentar las bases de una nueva manera de estudiar la naturaleza. Con metodología semejante a la de Arquímedes, Galileo habló a una época más madura; a diferencia de Leonardo, no escribió "al revés" y fue leído y, desde luego, criticado por sus contemporáneos.
La contribución de Galileo a la dinámica de los fluidos fue profunda, aunque indirecta, al participar en la fundamentación de la mecánica, de la física y de la ciencia misma. La astronomía fue la motivación de su trabajo y la pasión de su vida. Afirmaba entender más de los cuerpos celestes que de los fluidos que observamos todos los días...
Un aspecto decisivo en el paso de la especulación aristotélica a la ciencia posgalileana fue la introducción de la observación como pilar y sustento de la razón. Para entender el mundo, la razón pura demostró su fracaso. Del muy joven Leonardo al anciano Galileo se ve un cambio único en la historia. En estos doscientos años se lleva a cabo el florecimiento resultante de los previos dos mil años de siembras y cuidados
III. 3. DEL HORROR AL VACÍO, AL AGUA SECA
Es claro que no puede culparse a Aristóteles del estancamiento intelectual que siguió a su muerte. Fue la dogmatización de sus ideas y la exclusión de su actitud crítica y dinámica, que predicó y practicó, lo que casi paralizó la evolución del conocimiento.
La concepción aristotélica en torno al vacío y la aceptación sin reservas de
ésta dominaron hasta mediados del siglo XVII. Según Aristóteles la
naturaleza tiende a llenar todos los espacios con cualquier medio a su alcance,
siendo el vacío una imposibilidad física. La frase horror vacui vino a
resumir esta creencia a través del tiempo, y se llegaron a inventar sustancias
como el éter, con propiedades inconmensurables, no factibles de ser
medidas, para "explicar" la presencia de espacios aparentemente vacíos.
La crítica, no es de sorprender, fue iniciada por Galileo. La generación que le sucedió la continuó y la resolvió.
El compañero inseparable de Galileo en los últimos tres meses de su vida fue Evangelista Torricelli (1608-1647). Tras de extender algunos trabajos de aquél en dinámica de proyectiles y de generalizar en forma brillante parte de la obra de Arquímedes, fue invitado a Florencia por el anciano Galileo para discutir y escribir sus últimas ideas. Así, Torricelli se vio expuesto a muy variadas especulaciones y proposiciones que, en su desafortunadamente breve carrera científica, desarrolló al suceder al maestro en su cátedra de matemáticas.
Torricelli se ocupó de diversos problemas en forma teórica y experimental. En el área de fluidos destacan sus estudios sobre el flujo de chorros que salen por el orificio de un recipiente, su descubrimiento del principio del barómetro de mercurio y su uso en el estudio de la presión atmosférica. Con estos trabajos logró, entre otras cosas, acabar con el mito de la imposibilidad del vacío. Uno de sus experimentos consistió en demostrar la existencia de la presión atmosférica y la forma de crear un vacío, usando un dispositivo como el que se muestra en la figura II. 5. Una variación de éste se describe a continuación.
Es fácil convencerse de que la atmósfera ejerce una presión igual en todas direcciones. Se requiere un vaso, una hoja de papel o de plástico, agua y una cubeta (para no salpicar todo, como sucede; cuando se intenta por primera vez). Encima del vaso bien lleno de agua se pone el trozo de plástico, cuidando de que no quede en el aire entre éste y el agua. El vaso puede invertirse lentamente sin que el agua se caiga, debido a que el aire empuja constantemente contra el plástico (Figura III. 4(a)). Para que la demostración sea más contundente puede sumergirse parcialmente el vaso invertido en una cubeta llena de agua y retirar el plástico; ¡el agua no se sale! (Figura III. 4(b)). En este caso el aire empuja hacia abajo sobre la superficie horizontal del agua con la misma presión que en el caso anterior lo hizo hacia arriba.
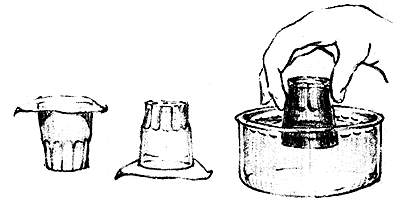
Figura III. 4. La presión atmosférica en la cocina.
Si el vaso mide más de 14 m de longitud (ji, ji), al realizar el experimento de la figura III. 4 (b), se saldría un poco de agua, quedando lo que parece una burbuja en el vaso. Ahí, en realidad, hay un razonable vacío; de hecho hay un gas (aire y vapor de agua) tan enrarecido como el que se encuentra a 200 km de altura sobre esta página (suponiendo que no es usted astronauta en funciones). Usando mercurio, basta con una columna de más de 76 cm de longitud para obtener un vacío equivalente; se ilustra en la figura II. 5, en el espacio de la parte superior del tubo.
Blaise Pascal (1623-1662) fue quien, repitiendo y extendiendo los experimentos de Torricelli, dio una clara explicación de las observaciones. Al darse cuenta de que los experimentos básicos podían ser explicados por igual en términos de la presión atmosférica en vez de en términos de un parcial horror al vacío, llevó a cabo un experimento de vacío dentro de otro vacío. De esta manera, al quitar la presión externa la altura de la columna de mercurio debía reducirse a cero, y así lo demostró, desechando la segunda explicación. No satisfecho, repitió los experimentos a diferentes alturas sobre el nivel del mar. Con ello probó que, si es la columna de aire que está arriba del dispositivo la que hace que el mercurio suba en el tubo, entonces la altura de éste debía cambiar según la cantidad de aire encima de él. Si a la naturaleza le daba horror el vacío, debía horrorizarle por igual ya fuera arriba o abajo de una montaña. Con esto quedó abandonada en forma definitiva la concepción del horror vacui.
En el proceso de estudio de la presión atmosférica Pascal inventó la prensa hidráulica, descubriendo el principio físico subyacente. Según éste la presión en un fluido actúa por igual en todas las direcciones; conocido como el principio de Pascal, es uno de los dos axiomas fundamentales de la hidrostática. El otro es el principio de Arquímedes. A los 31 años de edad y siendo una celebridad por sus variadas contribuciones en física y matemáticas, Pascal se convirtió en asceta; dedicó sus últimos ocho años de vida a la teología con la misma intensidad que dedicara antes a la ciencia.
Unos días antes del primer aniversario de la muerte de Galileo, en el pueblito inglés de Woolsthorpe, nació Isaac Newton (1642-1728). Como Da Vinci en su época, la luz de Newton brilla por encima del estrellado cielo de sus contemporáneos.
En agosto de 1665 la peste obliga a las autoridades a cerrar el Trinity College de Cambridge y Newton, cuatro meses después de su graduación, se ve obligado a regresar a su aldea natal. Ahí, aislado por dos años, lleva a cabo una hazaña sin paralelo en la historia del pensamiento humano. Lo que necesita y no sabe, lo inventa; lo que sabe y no le sirve, lo generaliza o lo cambia sin pudor alguno; sobre lo que no entiende, medita, observa, hace experimentos y propone hipótesis. Al final de este periodo ha cimentado sus tres contribuciones fundamentales: el cálculo infinitesimal, la mecánica y la gravitación, y la teoría de la luz y los colores. Así, aquel joven común y corriente que se fue, regresa convertido en el profundo pensador que sentaría las bases de la física y las matemáticas de los siguientes siglos.
Característico de la revolución científica del siglo XVII, y en
la mejor tradición cartesiana de la época, partió de la base de un universo real
cuyo comportamiento podía y debía ser explicado solamente en términos de sus
elementos y sus relaciones. Sobre esta base filosófica desarrolló la herramienta
matemática requerida y formuló las leyes de la mecánica. Su trabajo
Philosophiae Naturalis Principia Mathematica, publicado hasta 1687, es,
además de su obra maestra, uno de los trabajos más importantes de toda la
ciencia moderna.
La contribución de Newton a los fluidos fue múltiple y a niveles muy diferentes. Abarcó desde sus fundamentos, en forma indirecta, hasta los meticulosos experimentos que llevó a cabo sobre vórtices (remolinos) y viscosidad (fricción interna).
Desde el punto de vista general, el marco teórico, el aparato matemático y las leyes físicas que Newton estableció, fueron, y siguen siendo, los ingredientes esenciales de la teoría de los fluidos. Estos elementos fueron una aportación fundamental, aunque indirecta, para el establecimiento final de la teoría que realizó la notable generación que le siguió, formada por Euler, dos de los Bernoulli, D'Alambert y Lagrange.
Su trabajo directamente conectado con fluidos comprende casi un tercio de los Principia. Esto resulta sorprendente si no se toma en cuenta que Newton busca establecer una teoría alternativa, en contenido, forma y consecuencias, a la cartesiana. Ésta, que domina el pensamiento de la época, era una imaginería mecánica verbal sobre esferas y vórtices en movimiento en un medio etéreo que todo lo embebía.
La demoledora crítica de la cosmología cartesiana, que Newton presenta como preámbulo a su "sistema del mundo", es a la vez un cuidadoso estudio del comportamiento de los fluidos. En éste destacan sus análisis teóricos y experimentales sobre el movimiento de un vórtice y la naturaleza de la fricción interna de los fluidos, apareciendo así la primera definición, estudio y cuantificación de lo que posteriormente se llamó la viscosidad de un fluido. La incorporación de este resultado, de suma importancia en la dinámica de fluidos, no sucedió sino hasta un siglo y medio después.
¡Cuántos hay todavía que, dedicados a los fluidos, no la entienden!
Salvo la revisión de las siguientes ediciones de sus obras, Newton dedicó el resto de su vida, que duraría aún más de cuarenta años, a toda suerte de actividades relacionadas con la organización y administración pública y académica. También, debido a su difícil personalidad, trabajó arduamente para hacerle la vida de cuadritos a más de uno.
Gran parte del trabajo de Newton ha sido extendido, completado y reformulado en varias direcciones a través del tiempo. En cuanto a los fluidos, algunos de los problemas que abordó siguen siendo objeto de numerosas investigaciones; un problema tan aparentemente simple como el determinar el patrón de flujo que resulta del movimiento de una esfera en un medio viscoso, continúa siendo un desafío en el campo de las matemáticas aplicadas.
A la muerte de Newton, en plena ilustración, tres brillantes hombres empiezan a dominar, extender y perfeccionar las herramientas analíticas nuevas y, al mismo tiempo, a explotar su utilidad en el campo fértil y abierto de los fluidos. Daniel Bernoulli (1700-1782) y Leonhard Euler (1707-1783), formados en matemáticas por Johann Bernoulli, padre del primero, elaboran una serie de trabajos que, junto con los desarrollados por Jean le Rond d'Alambert (1717-1783), culminan con la formulación explícita de los principios generales y las ecuaciones básicas de la mecánica de los fluidos.
Las contribuciones más importantes de Bernoulli aparecieron en el año de 1738 en su libro Hydrodynamica, cuando se acuña el término. Entre ellas destaca el teorema que ahora lleva su nombre y que fue la primera formulación del principio de la conservación de la energía para el caso de los fluidos. En su versión moderna, cuya formulación general y correcta se debe a Euler, establece que la suma de tres cantidades es igual a una constante:
A + B + C = constante;
los sumandos corresponden a tres formas particulares de energía. El primero tiene que ver con el estado de movimiento, el segundo con la altura a la que se encuentra y el tercero con la presión. Si la suma de estas cantidades ha de permanecer constante es preciso que al aumentar una de ellas, al menos una de las restantes se vea disminuida en la proporción adecuada. Una restricción del teorema es que los efectos de fricción interna (viscosidad) y de compresibilidad en el fluido sean despreciables, es decir, muy pequeños. Bernoulli, con el sólido juicio de un científico de su estatura, además de subrayar la "maravillosa utilidad" de su teorema, advertía del error que podría traer su abuso o el olvido de sus limitaciones, las cuales eran si acaso intuidas.
Más técnicamente, los términos que aparecen en el teorema de Bernoulli son la energía cinética (A), la energía potencial (B) y la entalpía (C). A depende de la velocidad, A = rv²/2 (r es la densidad y v la velocidad); B depende del peso y su altura relativa, B = rgz (g es la aceleración de la gravedad y z la altura relativa a un nivel de referencia) y C depende de la presión, C = p, siendo p la presión.
Así, cuando una masa de agua desciende, disminuyendo la altura y por consiguiente el sumando B, la velocidad aumenta de manera tal que el sumando A crece lo suficiente para balancear la suma. De igual modo, en un tubo horizontal (Figura III. 5) en que el término B permanece fijo (z no cambia), la suma de A y C es la relevante. Puesto que en cada sección del tubo (s1 y s2) la cantidad de fluido que pasa es la misma, en la región más estrecha (s2) la velocidad debe ser mayor que en la más ancha (s1). De acuerdo con el teorema de Bernoulli, la presión es menor en donde la velocidad es mayor, es decir, en la zona angosta.
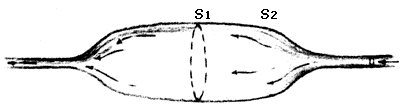
Figura III. 5. Tubo que se estrecha.
La situación parece irse haciendo un tanto tediosa. Como difícilmente podría ponerse peor, le solicito seguir leyendo un poco más para ver algunos casos en los que la aplicación del teorema es más interesante y que son fáciles de comprobar en un centro de investigación bien equipado, por ejemplo una cocina.
Imagine un tubo vertical por el que sale un chorro de aire (Figura III. 6(a)), por ejemplo, el tubo de una aspiradora casera conectado por la parte de atrás. Al poner una esfera ligera, digamos una pelota de pingpong, dentro del chorro ascendente, ésta permanece ahí sin caer. La razón es que la presión del aire en el chorro (cuya velocidad es grande) es menor que la del aire fuera de éste (con velocidad baja). Cuando la pelota empieza a salir de la corriente, la presión exterior, mayor a la interior, la regresa al chorro. El otro efecto, superpuesto al anterior, es la competencia entre el empuje del chorro, hacia arriba, y el peso de la esfera.
Un caso análogo es el de un pulverizador (Figura III. 6(b)). Cuando se sopla por un tubo (t) que termina en punta, el aire aumenta su velocidad al llegar a la punta y en consecuencia pierde presión. En la boca del tubo (e) se encuentra entonces aire cuya presión es menor a la que hay en su interior, que es la atmosférica y tiende a salir. La superficie del líquido en el recipiente (s) tiene una presión igual a la atmosférica, excepto la parte contenida en (e). Esto da lugar a que el líquido dentro del recipiente suba por el tubo. Al llegar a la salida, donde hay un chorro de aire, es arrastrado por éste y se pulveriza formando gotas minúsculas.
Usando el mismo razonamiento anterior puede explicarse el hecho de que al suspender dos esferas ligeras cercanas una de la otra y soplar en medio de ellas, se aproximen y choquen entre sí, como si apareciera una fuerza de atracción (Figura III. 6 (c)).
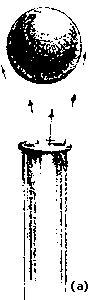
|
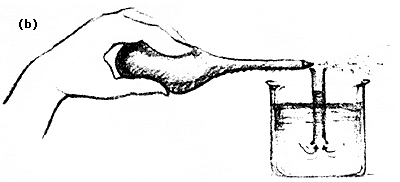
|
|
|
Figura III. 6. Explicaciones "a los Bernoulli". (a) Pelota en un chorro, (b) pulverizador, (c) "atracción" entre esferas.
Esta atracción aparente, debida a la distinta distribución espacial de presiones, que es sencilla de explicar invocando el teorema de Bernoulli, es el origen de múltiples fenómenos que de otra manera parecen incomprensibles. Entre ellos destaca la atracción entre automóviles y barcos que viajan paralelos. Cuando un automóvil rebasa a un camión de grandes dimensiones, es necesario sostener el volante con cierta fuerza; si se deja el volante libre, el automóvil se moverá hacia el camión (no es muy recomendable realizar este experimento).
Los capitanes de grandes barcos conocen este efecto; los que no, tienen ahora otra actividad de naturaleza terrestre. Un caso conocido es el de los barcos Olympic y Hauk. El primero, un transatlántico de grandes dimensiones, navegaba tranquilamente en mar abierto durante el mes de octubre de 1912. El segundo era un acorazado, pequeño en relación al Olimpic, que navegaba con una velocidad mucho mayor y en forma paralela (Figura III. 7(a)). Al encontrarse a una distancia de unos cien metros sucedió algo imprevisto, que no tuvo nada que ver con saludos mutuos. El Hauk cambió de rumbo en forma intempestiva y se dirigió directo al Olympic, sin que el timón sirviera para evitar la colisión (Figura III. 7(b)). La proa del acorazado se hundió en el casco del gran buque, abriendo una aparatosa vía de agua. Al margen de la incapacidad del tribunal marítimo que juzgó el caso y culpó al capitán del Olympic por no dar paso al acorazado, lo que ocurrió fue precisamente un caso de atracción hidrodinámica. Entre los barcos se formó un "canal" por donde el agua pasó más rápido que en la región exterior, esto en ambos barcos, que se consideran fijos (Figura III. 7(a)). La diferencia de presiones entre la zona interna y la zona externa produjo una fuerza que se puso de manifiesto en el barco más pequeño.
|
|
Figura III. 7. (a) El Olympic alcanza al Hauk. (b) Resultado de la atracción hidrodinámica.
El teorema fue sólo una de las aportaciones de Bernoulli. El original enfoque que dio el planteamiento y solución de diversos problemas fue de gran valor para el desarrollo de la naciente disciplina y constituyó un vigoroso estímulo para las brillantes dotes de algunos de sus contemporáneos y amigos.
En 1755 aparecen, una tras otra, las obras clásicas de Euler sobre los fundamentos de la mecánica de los fluidos. El genio matemático más notable del siglo había asimilado por completo la obra newtoniana y lo había plasmado en un lenguaje mucho más elegante y preciso. Formuló las ecuaciones diferenciales de movimiento en su forma general, deduciendo a partir de ellas los resultados previos ya conocidos, como el teorema de Bernoulli, dándoles su verdadera dimensión y generalidad. Posteriormente, exploró un gran número de consecuencias y atacó múltiples problemas de carácter práctico asociados a la maquinaria hidráulica, particularmente la turbina, la resistencia sobre barcos y la propulsión.
La copiosa correspondencia entre Euler, D'Alambert y Lagrange, entre otros, permite entender el interés que tenían las mejores mentes analíticas de la época por los problemas asociados a los fluidos. D'Alambert, que gozó la cima de las matemáticas francesas, dedicó la segunda parte de su vida a estudios de carácter experimental. Después de introducir diversos conceptos y métodos analíticos en sus dos obras básicas sobre fluidos, demostró lo que se conoce como la paradoja de D'Alambert. Como consecuencia de las ecuaciones de Euler, que ignoraban la existencia de la viscosidad, resultaba que la fuerza que sufre un obstáculo inmerso en una corriente era nula; es decir, el objeto no era arrastrado por el flujo. Para D'Alambert era claro que este resultado matemático estaba en franca contradicción con sus observaciones y que el problema debía estar en alguna de las premisas de la teoría. En forma consistente subrayó la primacía que el experimento debía tener sobre la teoría. Argumentos diversos de Euler y de Lagrange, para aclarar la paradoja, no pudieron convencerlo. La formulación matemática de la teoría hacía imposible que a un fluido en movimiento se le pidiera adherirse a la superficie de un sólido en reposo.
Como consecuencia de haber ignorado la fricción interna de los fluidos se tenía el peculiar resultado de que los fluidos no mojaban las paredes... ¡La hidrodinámica era el estudio del agua seca!
III. 4. EL SIGLO SINCRÉTICO
En los cien años comprendidos entre 1750 y 1850 se sentaron las bases teóricas y experimentales de la mecánica de los fluidos. Ese siglo sirvió para resumir, ordenar y extender el conocimiento que sobre los fluidos se había acumulado durante miles de años. Desde entonces hasta la fecha la tarea ha sido la de extraer de estos principios, formulados en forma matemática, la información necesaria para poder entender y predecir el comportamiento de los fluidos.
En la primera mitad de este notable periodo aparecieron, junto a las históricas obras de carácter teórico, una serie de memorias clásicas de cuidadosos trabajos experimentales. Destacan el veneciano Giovanni Poleni (1683-1781), el inglés John Smeaton (1724-1792) y la escuela francesa, en particular Henri de Pitot (1695-1771), Antoine Chézy (1718-1798), Jean Charles de Borda (1733-1799), el mismo D'Alambert, Charles Bossut (1730-1814) y Pierre Louis George DuBuat (1734-1809).
Es embarazoso limitar la lista de nombres y, más aún, no mencionar algunos de los detalles que hicieron de sus contribuciones un párrafo hermoso en las páginas de la investigación. Así, con la frente baja y ofreciéndoles nuestra admiración, diremos que sus esfuerzos y logros no fueron en vano. Los estudios que dejaron sobre la fuerza de flujos sobre obstáculos, sobre la salida de fluidos a través de orificios, sobre el cauce de canales y ríos, ondas y olas, máquinas hidráulicas de la más diversa índole y más, fueron el cimiento de las obras futuras. Sus experimentos fueron nuevos y determinantes, como lo fue el análisis de los datos y su interpretación al usar conceptos originales y más sencillos, abriendo así el panorama para las correctas e importantes generalizaciones que establecieron.
El periodo de gestación asociado a los últimos cincuenta años del siglo
XVIII no se limitó, desde luego y antes bien al contrario, a los fluidos,
a la parte académica o a la intelectual. La sociedad estaba fraguando una lucha
contra el hambre, contra la injusticia y por la libertad e igualdad. Así, se
entiende la intensa actividad que se aprecia en los fluidos; nada sorprende pues
que Lagrange visitara a Voltaire a instancias de D'Alambert y que este último
dirigiera y participara en una extensa obra de coordinación y planeación de vías
fluviales, navegación y canalización en toda Francia.
La explosión revolucionaria francesa, la primera República, Robespierre y Danton, la aventura napoleónica, la reinstauración de la República y tantos hechos, aparecen reflejados en todo. También en la revolución asociada a los fluidos.
Con la segunda etapa, correspondiente a la primera mitad del siglo XIX,
concluye el nacimiento de la mecánica de los fluidos. Mucho se ha hecho
desde entonces y mucho, seguramente mejor, habrá de hacerse en el futuro. La
criatura nació y creció, llegando a su infancia al empezar el último siglo del
milenio. Veamos cómo acabó de formarse y qué dones (y defectos) trajo al mundo.
Para hablar de su madurez habrá que esperar, al menos, un ratito.
Desde el punto de vista experimental, el siglo XIX se inició con
una sólida tradición. Se contaba con una gran variedad de técnicas y métodos muy
confiables y, en consecuencia, de resultados razonablemente precisos, en
especial sobre la resistencia de obstáculos a un flujo. La hidráulica había
avanzado en forma casi independiente de la hidrodinámica teórica. En cierto
sentido, caminaban por veredas distintas, aunque paralelas, compartiendo
problemas y perspectivas pero difiriendo en métodos, prioridades y lenguaje.
El consenso en torno a lo equivocado que era ignorar los efectos de la viscosidad se había alcanzado en la primera década del naciente siglo. Sin duda, Newton y algunos de los que le siguieron se dieron cuenta de la necesidad de incorporar el efecto y así lo comentaron en sus obras. Sin embargo, sus intentos para lograrlo fueron infructuosos.
En 1821 se presentó ante la Academia de Ciencias, en París, un trabajo de Claude Louis Marie Henri Navier (1785-1836), ingeniero de formación y vocación. En éste se deducían las ecuaciones fundamentales de la elasticidad, que hoy en día llevan su nombre, para describir el equilibrio y las vibraciones en un sólido. Estas resultaban de un análisis puramente matemático en el que los átomos, entonces entes hipotéticos, se imaginaban como partículas que interactuaban por medio de resortes. No sorprende que fuese Navier el primero en construir un puente colgante a partir de un proyecto y de un cálculo; previamente las construcciones se hacían sobre bases empíricas.
Un año después, Navier presentó una memoria en la que, guiado por una analogía formal con la teoría de la elasticidad, deducía por primera vez las ecuaciones que incorporaban la viscosidad en la dinámica de un fluido. Como caso especial, el fluido ideal o invícido (que no presenta fricción interna), recuperaba las ecuaciones de Euler; en el caso general, las ecuaciones eran de una naturaleza esencialmente distinta. Desafortunadamente, la deficiente interpretación que dio a sus resultados, al resolver ciertos casos, le impidió explorar su notable contribución. Aun así, el agua, y todos los fluidos, ¡habían empezado a mojar!
Las ideas de Navier sobre la atracción y repulsión entre las moléculas, como origen de la viscosidad, fueron seguidas y ampliadas por dos excelentes matemáticos de la época: Simeon Denis Poisson (1781-1840) y Agoustin Lonis de Cauchy (1789-1857). El carácter especulativo de las hipótesis "microscópicas" que usaron le da a sus trabajos en este particular un interés sólo histórico.
Siguiendo una argumentación totalmente distinta y en términos de conceptos puramente macroscópicos, evitando todo lo relativo a la constitución última de un fluido, Jean Claude Barré de Saint Venant (1797-1886) dedujo las mismas ecuaciones de Navier. Su trabajo publicado en 1843, contiene una deducción semejante a la que hoy en día se sigue para obtener las ecuaciones; ese crédito nunca lo recibió. La fama de Saint Venant provino de sus múltiples trabajos en elasticidad, ya que en hidrodinámica su nombre no fue asociado ni a las ecuaciones que obtuvo, ni a diversos resultados que posteriormente fueron encontrados por otros investigadores, particularmente de Inglaterra.
El Imperio británico, en plena expansión y en la víspera de su apogeo, fue el ámbito donde la teoría y los experimentos alcanzaron la cumbre. Pasadas las guerras napoleónicas y con la República francesa en proceso de consolidación, la hegemonía política pasa a la sede del imperio; el dominio académico también. Mientras se consolidan, controlan y explotan las colonias africanas, americanas y asiáticas, que incluyen a cerca de la cuarta parte de la población y superficie del planeta, las ciencias florecen otra vez, sobre la fértil tierra de una tradición sólida y rica. Técnica y ciencia retroalimentan a la Revolución Industrial que, en estos cien años que hemos considerado sincréticos, nace, madura y se extiende.
En ese empono económico y cultural brilla, con otros distinguidos científicos, George Gabriel Stokes (1819-1903). Este matemático y físico irlandés, quien se educó y vivió en Cambridge casi toda su vida, fue el primero en ocupar, después de Newton, la cátedra lucasiana de física y los puestos de secretario y presidenter de la Sociedad Real de Física.
Entre sus numerosos trabajos, en muy diversos campos de las matemáticas; y la física teórica y experimental, destacan los que versan sobre: la dinámica de los fluidos viscosos. En la parte que concierne a los fundamentos de esta última, el joven Stokes llevó a cabo una elegante deducción de las ecuaciones que primero obtuviera Navier, en una memoria presentada ante la Sociedad Real en 1845. Su razonamiento, análogo al de Saint Venant, fue totalmente fenomenológico, eludiendo especulaciones en torno a la constitución microscópica de los fluidos.
Postulando como principios generales la conservación de la masa y el momento lineal (la segunda ley de Newton), como lo hicieran antes Bernoulli y Euler, lleva a cabo un cuidadoso análisis de las fuerzas que puede experimentar una pequeña parte de fluido. Fue importante la separación que hizo entre las fuerzas que dependen de la masa de fluido en consideración, como el peso (atracción gravitacional), y las que dependen de la superficie de la muestra, que son las responsables de la fricción (recordemos que los raspones los lucimos en la piel). Así, Stokes construyó una expresión para estas últimas que era la generalización de los estudios que había hecho Newton al respecto, ya casi olvidados con el tiempo.
El resultado clave fue encontrar que la fuerza de fricción de una parte de fluido sobre otra depende de la velocidad con la que se mueve una respecto de la otra; en términos más técnicos, se diría que la fuerza de fricción, por unidad de área, depende linealmente del gradiente de la velocidad (es decir, de la forma en que varía la velocidad de un punto a otro); qué tan estrecha es esta relación lo determina un factor constante llamado el coeficiente de viscosidad. A diferencia de Navier y de Saint Venant, Stokes analizó y resolvió las ecuaciones para algunos casos, obteniendo los primeros resultados que podían ser contrapunteados exitosamente con los experimentos. Las ecuaciones llevan ahora el nombre de Navier Stokes.
Sería difícil hallar a un científico cuyo nombre esté asociado a mas resultados que el de Stokes. En matemáticas hay un importante teorema que lleva su nombre, en fluidos las ecuaciones básicas llevan su apellido, al igual que una ley de movimiento para esferas y una paradoja; en óptica, unas líneas espectrales y el corrimiento de la luminiscencia son sus hijas registradas y bautizadas.
Con el establecimiento de las ecuaciones básicas, el éxito de las primeras e importantes aplicaciones de ellas, el gran cúmulo de precisas observaciones y el desarrollo de muy diversos métodos de investigación experimental y analítica, la ciencia de los fluidos tomaba la forma que tiene tal y como hoy la conocemos. Los cimientos del trabajo de las generaciones futuras estaban completos.
III .5. MATRIMONIO POR CONVENIENCIA
Una visión antropomórfica de la ciencia de los fluidos nos puede ayudar a entender la situación.
Se podría pensar que con las bases de la teoría bien establecidas, una
sistemática educación daría a la criatura una madurez de brillante
productividad. Como suele suceder, lo que podía salir mal, salió mal. Apareció
un problema que hasta la fecha no ha sido resuelto satisfactoriamente: las
matemáticas necesarias para resolver las recién descubiertas ecuaciones (no
lineales) no se habían desarrollado (¿inventado?, ¿descubierto?...). Así, al
comenzar la segunda parte del siglo XIX , los interesados en la
hidrodinámica se encontraron con un problema claramente planteado pero con
insuficientes herramientas para resolverlo.
No es de sorprender que el mismo Stokes iniciara uno de los enfoques para abordar el problema. "Si no puedes agarrar al toro por los cuernos, ¡corre!", dice un adagio azteca, y así lo hizo. Argumentado cuidadosamente, simplificó las ecuaciones de manera que pudiera domesticarlas y sacarles provecho. Los resultados que obtuvo por la aproximación tuvieron tal éxito que hoy en día se siguen explotando estas mismas ecuaciones que, desde luego, también llevan su nombre. Su análisis del movimiento de una esfera en un líquido sigue siendo uno de los resultados clásicos de la mecánica de fluidos; la expresión que relaciona a la fuerza que arrastra a la esfera con el producto de la velocidad de la corriente, el radio de la esfera y la viscosidad del fluido, se conoce como la ley de Stokes. La utilidad de un resultado tan "simple" como éste ha sido amplia y de la más diversa índole
Un problema representativo de los fluidos fue (y sigue siendo) el de
establecer el flujo en tuberías. Por evidentes razones prácticas había sido
objeto de innumerables estudios teóricos y experimentales. Hasta que no se
incorporó el efecto de la viscosidad, la teoría correspondiente se había
reducido a ejercicios pintorescos en matemáticas "no aplicadas".
Experimentalmente, fue el siglo XIX el que vio los primeros
resultados correctos sobre el flujo en un tubo, lo que no deja de llamar la
atención por el uso que de acueductos, drenajes, fuentes y tuberías en general
había anteriormente.
Entre otros, destacan los trabajos de Gotthilf Heinrich Ludwig Hagen (1797-1884) y de Jean Louis Poiseuille (1799-1869). El primero fue un distinguido ingeniero alemán cuyas contribuciones recibieron la injusticia de la historia; nunca recibió el crédito por su trabajo. Poiseuille fue un médico interesado en la fisiología de aparato cardiovascular que, para caracterizar el flujo sanguíneo, llevó a cabo cuidadosos experimentos en tuberías muy delgadas (tubos capilares) para determinar la forma del flujo, la resistencia de éste y la descarga. De esta manera estableció que la cantidad de líquido que pasa por un tubo cada segundo depende de la carga (la diferencia de presiones por unidad de longitud) y de la cuarta potencia de su diámetro (el diámetro multiplicado por sí mismo cuatro veces). Veinte años más tarde se desarrolló el primer análisis teórico que explicaba las observaciones de Poiseuille. Franz Neumann (1798-1895) y Eduard Hagenbach (1833-1910), en forma independiente, obtuvieron las expresiones para la forma (parabólica) del flujo y para la descarga, que se ajustaban bien a los datos conocidos; Hagenbach, al citar sólo a Poiseuille sin mencionar a Hagen, inició la discriminación de su compatriota.
Vale la pena hacer notar que el problema aún está lejos de resolverse. Una
gran cantidad de trabajos experimentales sobre el flujo en tuberías se sigue
publicando en la bibliografía especializada; innumerables tablas empíricas se
han publicado para su uso en el diseño de sistemas de drenaje, plantas
industriales de diferentes características, etc., y complicadas relaciones entre
parámetros del flujo siguen siendo elaboradas. Para las condiciones que se dan
en la práctica, el movimiento de un líquido es sumamente complicado y la teoría
ha sido, hasta la fecha, incapaz de dilucidar el problema. Las predicciones
teóricas del siglo XIX, desde luego aproximadas, han podido
mejorarse muy poco.
Muchas contribuciones previas y subsecuentes a las de Navier y de Stokes merecerían un libro cada una. Sin embargo, aquí el propósito ha sido el de delinear la forma en que se establecieron los principios básicos. Es conveniente recalcar que la hidráulica, que escuetamente sería el manejo de los fluidos, gozó del mismo vertiginoso avance que la hidrodinámica, su contraparte teórica. Aquí sólo hemos esbozado el crecimiento de esta última. Sin embargo, el desarrollo paralelo de ambas, independiente hasta cierto punto, llevó a la pareja a la edad del cortejo... Si bien se conocían desde la infancia, como suele suceder, hubo etapas en que se hablaban poco, cuando no es que se odiaban, especialmente al obligarlos a estar juntos. Antes de entrar en la parte que concierne al romance, vale la pena describir algunos rasgos de una de las partes comprometidas.
Por un lado, son notables las teorías de vórtices que desarrollaron Hermann Ludwig Ferdinand von Helmholtz (1821-1894), Gustav Robert Kirchhoff (1824-1887) y William Thomson (1824-1907), más conocido por su título nobiliario de lord Kelvin. Destacan también las obras de Joseph Boussinesq (1842-1929) y de John William Strutt (1842-1919), el famoso lord Rayleigh. El primero de éstos desempeñó el papel que Fernando de Rojas diera a Celestina; sus rigurosos estudios analíticos fueron siempre contrastados con los datos y las observaciones, subrayando las virtudes de una relación duradera entre la hidráulica y la hidrodinámica. Rayleigh, versátil como algunos de sus brillantes contemporáneos, abordó problemas que siguen siendo una muestra del claro pensar de una exitosa generación de científicos; su teoría de la propagación del sonido es sólo un ejemplo.
Un protagonista singular de esta época es Osborne Reynolds (1842-1912). Estudiando casi los mismos problemas que Boussinesq, cultivó el otro lado de la relación que nos ocupa, la hidráulica. Aun así, cada uno destacó en la contraparte; Reynolds se sublimó en la hidrodinámica. Sus meticulosos trabajos experimentes eran delicadamente contrapunteados con resultados analíticos; algo parecido a lo que Mozart hubiese logrado si en lugar de componer su exquisita e insuperable música se hubiera concentrado en jugar con charcos y la teoría correspondiente. ¡De lo que se perdieron los fluidos y lo que ganamos todos!
Reynolds, prototipo del profesor distraído, introdujo conceptos y métodos que siguen siendo aprovechados por quienes nos ganamos el pan con los fluidos. Como "para muestra basta un botón", caracterizó la forma en que un fluido pasa de un estado de movimiento laminar (regular) a uno turbulento (caótico), introduciendo, entre otras cosas, un parámetro adimensional conocido ahora como el número de Reynolds.
La idea básica es como sigue. Una madre ingeniosa decide jugar en la cocina de su casa con unos popotes. A pesar de las protestas de su familia, averigua cómo se mueve el jugo de mandarina en su "dispositivo experimental" y, como es de suponerse publica un artículo sobre el tema. Meses más tarde y en otro país, en una oficina con poca luz, un ingeniero del Departamento de Aguas debe rediseñar el sistema de drenaje de un barrio, dentro del cual se encuentra su casa; es decir, le interesa que funcione. ¿Le sirve lo que escribió la susodicha mamá? Ella trabajó con el jugo de un cítrico, tubos de plástico y una sana curiosidad; él debe hacerlo con... otros materiales. Gracias a la dama y a Reynolds, el ingeniero puede evitar hacer pruebas costosas y, tal vez, desagradables.
Supóngase que U es la velocidad media del fluido en un tubo, D el diámetro de éste y v la viscosidad del fluido. Lo que Reynolds encontró fue que si el valor numérico del producto de U y D, dividido por v, es el mismo para dos sistemas, aunque parezcan muy distintos, ¡el flujo será el mismo!. Cosas como el gasto, el carácter laminar o turbulento, etc., serán iguales. Lo que tiene que hacer el ingeniero es ver si su sistema escala adecuadamente.
Si el diámetro de los tubos del drenaje es de 2 m y el de los popotes es de 0.5 cm, parecería no haber mucha relación. Digamos que la viscosidad del jugo de mandarina es de aproximadamente .01 cp y la de lo que se mueve en el drenaje es de cerca de 1 cp (unas cien veces más viscoso); cp es la abreviatura del centipoise (pronúnciese "sentipuazz"), la unidad de medición de la viscosidad. Entonces, para que los números de Reynolds de cada caso sean iguales, basta con que la velocidad del jugo en los popotes sea cuatro veces la del "fluido" en el drenaje. Además de ser más barato el experimento casero, la vitamina C es mucho más saludable.
Es justamente en este hecho, el principio de semejanza, que está basado el modelado hidro y aerodinámico. Cuando se hacen maquetas de muelles, de rompeolas, de aviones o de submarinos, además de divertirse, los investigadores (ingenieros, físicos o matemáticos) se están ahorrando tiempo, esfuerzo y (a sus patrones) muchos kilogramos de oro. Si el juguetito flota, el buque tanque de 100 000 toneladas también lo hará..., si es semejante.
Al iniciarse el siglo XX, el cortejo entre la hidrodinámica y la
hidráulica parecía no tener futuro alguno; los intereses comunes o bien se
expresaban en lenguajes diferentes o parecían inútiles o muy complicados. Las
obras de Horace Lamb y de A. A. Flamant ilustran bien la situación; la primera
cubre los aspectos teóricos y la otra los experimentales, con poco material
común. La hidrodinámica se interesaba principalmente en los flujos invícidos o
ideales, lateralmente en los flujos viscosos laminares y no hacía caso de los
flujos turbulentos, siendo esta última la característica más importante para la
hidráulica. Así, las excelentes virtudes de una disciplina eran ignoradas por la
otra.
En estas condiciones, en 1904, se presentó un trabajo experimental, en un congreso de matemáticas, en la ciudad de Heidelberg, Alemania. El autor, un brillante ingeniero llamado Ludwig Prandtl (1875-1953), iniciaba una conspiración para unir a la caprichosa pareja. A raíz de esa participación, Prandtl fue invitado a trabajar y colaborar en uno de los ambientes más estimulantes y fértiles para la investigación de que se tiene memoria. Con ese trabajo, titulado Sobre el movimiento de fluidos con viscosidad pequeña, empezaba una profunda revolución mecánica de fluidos.
El punto esencial de la contribución de Prandtl, elaborado en una secuencia de publicaciones a lo largo de una década, y que sólo es parte de su variada obra acerca de los fluidos, fue el siguiente.
La dificultad era que la hidrodinámica, ese elegante aparato matemático que estudiaba sobre todo a los fluidos ideales, describía muy bien una parte importante del movimiento real de los fluidos, como la forma de la estela que deja tras de sí un objeto inmerso en una corriente. Por otra parte, predecía algunos casos claramente absurdos, como la inexistencia del arrastre de la corriente sobre el objeto inmerso en ella, en franca contradicción con las observaciones (y la experiencia de los ahogados en torrentes por todo el mundo).
La solución ahora parece mas o menos obvia, como siempre sucede con los problemas una vez resueltos. Si la teoría de los fluidos ideales no podía describir correctamente el movimiento de los fluidos reales cerca de cuerpos sólidos, debía haber una forma de tomar en cuenta los efectos de la viscosidad en la inmediata vecindad de las paredes de éstos. Es decir, muy cerca de una superficie sólida debía existir una región, que Prandtl bautizó como la capa límite, en la que dominaran los efectos viscosos; fuera de ella, la descripción del modelo de fluidos ideales debía ser suficiente. De esta manera, el problema se reduce a simplificar las ecuaciones de Navier-Stokes lo necesario como para poder resolverlas dentro de la capa límite; fuera de ésta, los resultados deben ser iguales a los del caso ideal.
Y así, Prandtl quiso, pudo e hizo. Haciendo ver las bondades de cada parte y las desventajas del celibato para una pareja tan potencialmente fértil, manipuló la situación y documentó (con teoría y experimentos) la conveniencia de ese matrimonio. El amor llegará después —les decía— y a la pareja la dejó bien casada. La prole sigue agradecida a Prandtl por las delicadas gestiones que hizo para abrir un horizonte que explorar, donde antes sólo parecía haber una oscuridad abisal.
Las contribuciones sobresalientes de Prandtl no quedaron ahí, ni fue éste el último de los brillantes investigadores en el tema; algunos de los que faltan, varias ideas y métodos, como las que abordan la turbulencia o el uso de las computadoras, aparecerán más adelante.
Con este panorama de la historia de los fluidos, un tanto cubierto de nubes, pero con suficientes claros que dejan entrever el hermoso paisaje, es mejor dejar a la mente descansar y a los ojos distraer. Es un buen momento para detener la lectura, estirar las piernas y mirar a un fluido de frente. Luego, viendo agua, aire o fuego, murmurar en silencio, (lo que no haríamos con un adolescente) "te voy entendiendo...".